第六章——堆排序
一 堆
堆给人的感觉是一个二叉树,但是其本质是一种数组对象,因为对堆进行操作的时候将堆视为一颗完全二叉树,树种每个节点与数组中的存放该节点值的那个元素对应。所以堆又称为二叉堆,堆与完全二叉树的对应关系如下图所示:
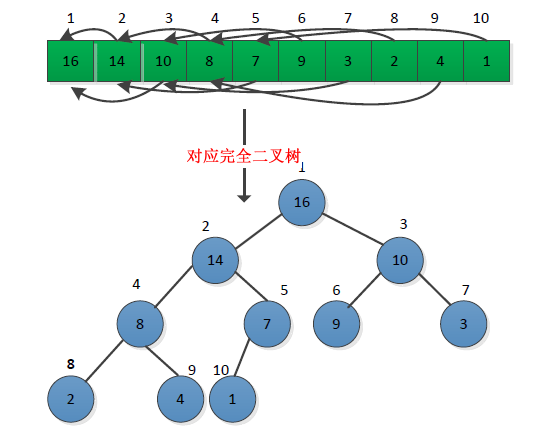
二叉堆可以分为两种形式:最大堆和最小堆。在这两种堆中,结点的值都要满足堆的性质。
在最大堆中,最大堆的性质是指除了根以外的所有结点i都要满足:
A[PARENT(i)]>=A[i]
也就是说,某个结点的值至多与其父结点一样大。因为,堆中的最大元素存放在根结点中;并且,在任一子树中,该子树所包含的的所有结点的值都不大于该子树根结点的值。最小堆的组织方法正好相反:最小堆性质是指除了根以外的所有结点i都有
A[PARENT(i)]<=A[i]
最小堆中的最小元素存放在根结点中。
在堆排序算法中,我们使用的是最大堆。最小堆通常用于构造优先队列、
如果把堆看成一棵树,我们定义一个堆中的结点的高度就为该结点到叶结点最长简单路径上边的数目;进而我们可以把堆的高度定义为根结点的高度。既然一个包含n个元素的堆可以看成是一颗完全二叉树,那么该堆的高度是O(lgn)。我们会发现,堆结构上的一些基本操作的运行时间至多与树的高度成正比,即时间复杂度为O(lgn)。
- MAX-HEAPIFY 过程:其时间复杂度为O(lgn),它是维护最大堆性质的关键。
- BUILD-MAX-HEAP过程:具有线性时间复杂度,功能是从无序的输入数据数组中构造一个最大堆。
- HEAPSORT过程:其时间复杂度O(lgn),功能是对一个数组进行原址排序。
- MAX-HEAP-INSERT、HEAP-EXTERACT-MAX、HEAP-INCREASE-KEY和HEAP-MAXIMUM过程:时间复杂度为O(lgn),功能是利用堆实现一个优先队列。
二 维护堆的性质
MAX-HEAPIFY是用于维护最大堆性质的重要过程。它的输入是一个数组arr和一个下标i和数组长度。通过让arr[i]的值在最大堆中”逐级下降“,从而使得以下标i为根结点的子树重新遵循最大堆的性质。
//递归的调整堆
void MaxHeapity(int arr[],int i,int n)
{
int lchild,rchild;
int largest;
lchild=LEFT(i);
rchild=lchild+1;
if(lchild<=n-1&&arr[i]<arr[lchild])
largest=lchild;
else
largest=i;
if(rchild<=n-1&&arr[rchild]>arr[largest])
{
largest=rchild;
}
//largest==i既可以判断要调整的点是否还存在左子树和右子树也可以判断要调整的节点的值是否大于其子树
if(largest!=i)
{
swap(&arr[largest],&arr[i]);
MaxHeapity(arr,largest,n);
}
}
三 建堆
我们可以用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n的数组arr[0..n]转换为最大堆。我们指定,子数组arr[n/2]...a[n-1]中的元素都是叶子节点。每个叶节点都可以看成只含有一个元素的堆。过程BUILD-MAX-HEAP对树中的其他结点都调用一次MAX-HEAPIFY。
//建堆
void BuildMaxHeap(int arr[],int n)
{
int i;
for((i=n/2-1);i>=0;i--)
{
MaxHeapity(arr,i,n);
}
}
四 堆排序算法
初始时候,堆排序算法利用BUILD-MAX-HEAP将输入数组arr[0...n-1]建成最大堆。因为数组中的最大元素总在根结点arr[0]中,通过把它与arr[n-1]进行交换,我们可以让该元素放到正确的位置。这时候,如果我们从堆中去掉结点n-1,剩余的结点中,原来根的孩子结点仍然是最大堆,而新的根结点可能会违背最大堆的性质。为了维护最大堆的性质,我们要做的是调用MAX-HEAPIFY(arr,0,n-1),从而在arr[0..n-2]上构造一个新的最大堆。堆排序算法会不断重复这一过程。直到堆的大小从n-1降到1.
//堆排序
void HeapSort(int arr[],int n)
{
int i;
BuildMaxHeap(arr,n);
for(i=n-1;i>0;i--)
{
swap(&arr[0],&arr[i]);
MaxHeapity(arr,0,i);
}
}
递归版本的代码:
#include<iostream>
using namespace std;
#define LEFT(i) (2*i+1)
void swap(int *a,int *b)
{
int temp=*a;
*a=*b;
*b=temp;
}
//递归的调整堆
void MaxHeapity(int arr[],int i,int n)
{
int lchild,rchild;
int largest;
lchild=LEFT(i);
rchild=lchild+1;
if(lchild<=n-1&&arr[i]<arr[lchild])
largest=lchild;
else
largest=i;
if(rchild<=n-1&&arr[rchild]>arr[largest])
{
largest=rchild;
}
//largest==i既可以判断要调整的点是否还存在左子树和右子树也可以判断要调整的节点的值是否大于其子树
if(largest!=i)
{
swap(&arr[largest],&arr[i]);
MaxHeapity(arr,largest,n);
}
}
//建堆
void BuildMaxHeap(int arr[],int n)
{
int i;
for((i=n/2-1);i>=0;i--)
{
MaxHeapity(arr,i,n);
}
}
//堆排序
void HeapSort(int arr[],int n)
{
int i;
BuildMaxHeap(arr,n);
for(i=n-1;i>0;i--)
{
swap(&arr[0],&arr[i]);
MaxHeapity(arr,0,i);
}
}
int main()
{
int arr[10]={19,88,3,5,7,39,79,37,8,9};
HeapSort(arr,10);
for(auto a:arr)
cout<<a<<" ";
cout<<endl;
}
非递归版本的代码:
#include<iostream>
using namespace std;
#define LEFT(i) (2*i+1)
void swap(int *a,int *b)
{
int temp=*a;
*a=*b;
*b=temp;
}
//非递归的调整堆
void MaxHeapity(int arr[],int i,int n)
{
int lchild,rchild;
int largest;
while((2*i+1)<n){
lchild=LEFT(i);
rchild=lchild+1;
if(lchild<=n-1&&arr[i]<arr[lchild])
largest=lchild;
else
largest=i;
if(rchild<=n-1&&arr[rchild]>arr[largest])
{
largest=rchild;
}
//largest==i既可以判断要调整的点是否还存在左子树和右子树也可以判断要调整的节点的值是否大于其子树
if(largest!=i)
{
swap(&arr[largest],&arr[i]);
i=largest;
}
else
break;
}
}
//建堆
void BuildMaxHeap(int arr[],int n)
{
int i;
for((i=n/2-1);i>=0;i--)
{
MaxHeapity(arr,i,n);
}
}
//堆排序
void HeapSort(int arr[],int n)
{
int i;
BuildMaxHeap(arr,n);
for(i=n-1;i>0;i--)
{
swap(&arr[0],&arr[i]);
MaxHeapity(arr,0,i);
}
}
int main()
{
int arr[10]={19,88,3,5,7,39,79,37,8,9};
HeapSort(arr,10);
for(auto a:arr)
cout<<a<<" ";
cout<<endl;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号