红黑树-结点的插入

红黑树介绍

红黑树本质上是一种二叉查找树，但它在二叉查找树的基础上额外添加了一个标记（颜色），同时具有一定的规则。这些规则使红黑树保证了一种平衡，插入、删除、查找的最坏时间复杂度都为 O(logn)。它的统计性能要好于平衡二叉树（AVL树），这也正解释了红黑树为什么使用这么广的原因。

红黑树的5个特性：

每个结点要么是红色，要么是黑色。
根节点永远是黑色的。
所有叶子结点(nil结点)都是黑色的。（这里说的叶子结点是NULL结点）
每个红色结点的两个子结点一定都是黑色（不能有两个连续(父-子连续)的红色结点，可以有连续的黑色结点）。
从任一结点到其子树中每个叶子结点的路径都包含相同数量的黑色结点。（黑高相同）

正由于平衡二叉树一样，由性质决定了二叉树是不是一个平衡二叉树，当向平衡二叉树插入一个结点后可能失衡的依据也是性质决定的，性质定义了什么是平衡二叉树。所以说，红黑树的性质解释了什么是红黑树，以及插入结点后，树是否还能保持红黑树的性质。

红黑树是一个自平衡（不是像AVL绝对的平衡）的二叉查找树BST，但是也是需要保持平衡，它不是像AVL那样，刻意的保持平衡，而是由红黑树的性质间接保持了Reb-Black-Tree的平衡，如不能有两个连续的红色结点，连续插入两个结点必然会使性质 4不成立，通过recolor或者rotation来满足性质4，调整的过程也间接使红黑树维持了相对平衡。如果熟悉了AVL如何调整平衡，那么我感觉Red-Black-Tree的调整平衡应该也不在话下。

如下图，就是一棵红黑树，NIL是一个黑色的空结点。

红黑树结点的插入

红黑树结点的插入操作：

红黑树本身是一棵二叉查找树，所以在插入新结点时，完全可以按照二叉查找树插入结点的方法，找到新结点插入的位置。
将插入的结点初始化为红色，为什么是红色而不是黑色？若为黑色，则违背性质5。
插入结点后，可能会破坏红黑树的性质，此时需要调整二叉查找树，通过recolor或者rotatin，使其重新成为红黑树。

红黑树的调整主要有两个操作，比AVL树多了一个操作：

recolor（变色，重新标记为黑色或红色）
rotation（旋转）

优先recolor，recolor不能解决在rotation。

红黑树中插入结点后，主要有3大种6小种：

红色结点作为根节点，涂黑，直接插入。
父结点是黑结点，直接插入红色结点。
父结点是红色结点，这时候直接插入红色结点，不满足性质4。这时候就需要根据其叔叔结点是红色还是黑色分别处理。（分为6小种）
- 叔叔结点是红色，uncle and parent discolor, 左右支处理情况相同
- 叔叔结点是黑色，父结点位于祖父结点的左分支，插入结点位于父结点的左分支，旋转加变色；插入结点位于父结点的右分支，旋转旋转加变色。
- 叔叔结点是黑色，父结点位于祖父结点的右分支，插入结点位于父结点的右分支，旋转加变色；插入结点位于父结点的左分支，旋转旋转加变色。

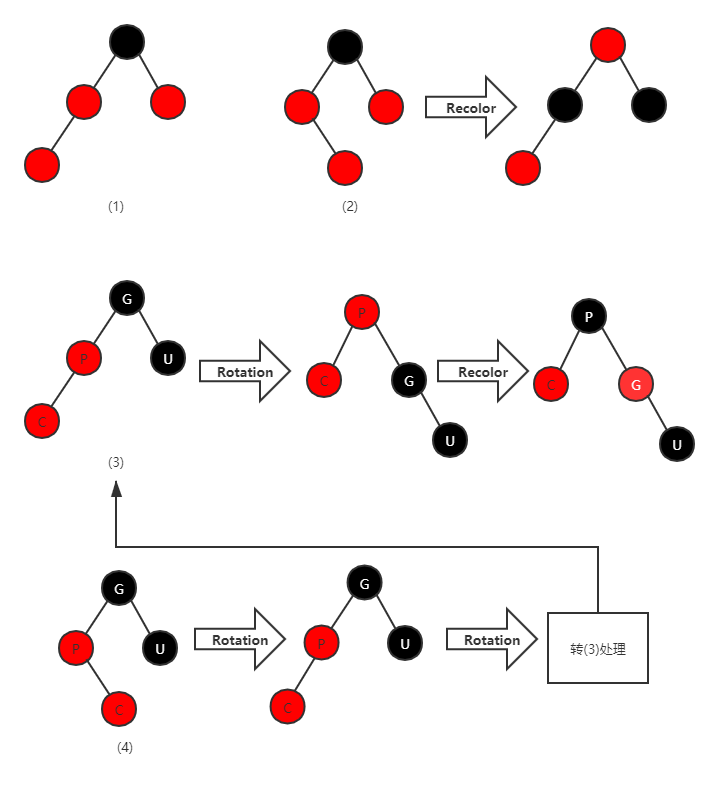
图(4)中存在一个错误，即旋转后P应该是C的子结点，代码中需要提前x = x->parent，然后下次循环时x->parent->parent才能正确处理。

图(3)中U也可以看做是NIL结点（空结点），对于图(1)根节点变红，这不是违背了性质2，代码最后对根结点做了处理，最后总会变黑的！

在看代码之前，我觉得有必要了解红黑树结构的代码定义以及初始化一棵红黑树。

#include <stdio.h>
#include <stdlib.h>

typedef enum {RED, BLACK} ColorType;
typedef int ElemType;
/*树结点类型定义*/
typedef struct RBNode {
    ElemType key;
    struct RBNode * lchild;
    struct RBNode * rchild;
    struct RBNode * parent;
    ColorType color;
} RBNode, *RBTree;

/*我把它理解为树的头结点*/
typedef struct RBTRoot {
    RBTree root;
    RBTree nil;
} RBTRoot;

/**
* 初始化一棵红黑树头结点
*/
RBTRoot* RBTree_Init() {
   RBTRoot* T = (RBTRoot*) malloc(sizeof(RBTRoot));
   T->nil = (RBTree) malloc(sizeof(RBNode));
   if (T == NULL || T->nil == NULL)
        exit(-1);
   T->nil->lchild = T->nil->rchild = NULL;
   T->nil->parent = NULL;
   T->nil->color = BLACK;

   T->root = T->nil;
   return T;
}

下面以插入元素{10,9,8,7,6,5,4,3,2,1}为例，查看红黑树如何从0构造为一棵树。结合动图看代码，我觉得能更容易理解代码：

首先插入元素10和9

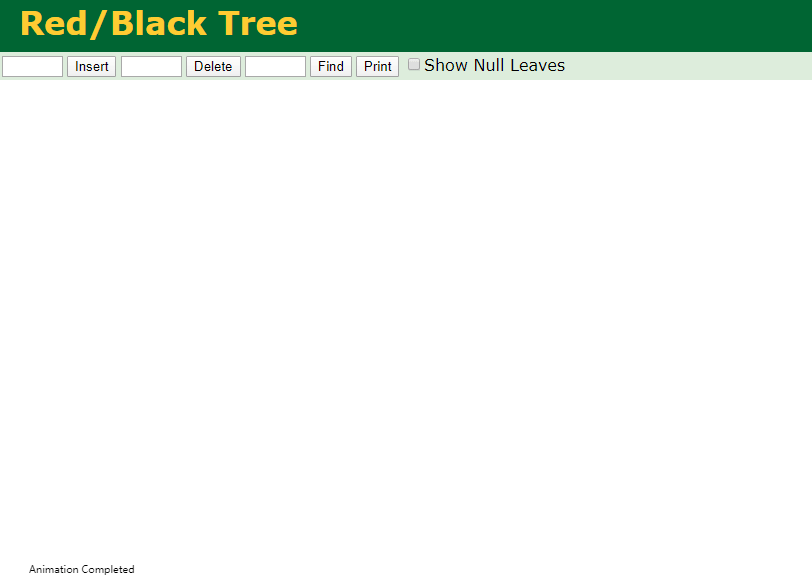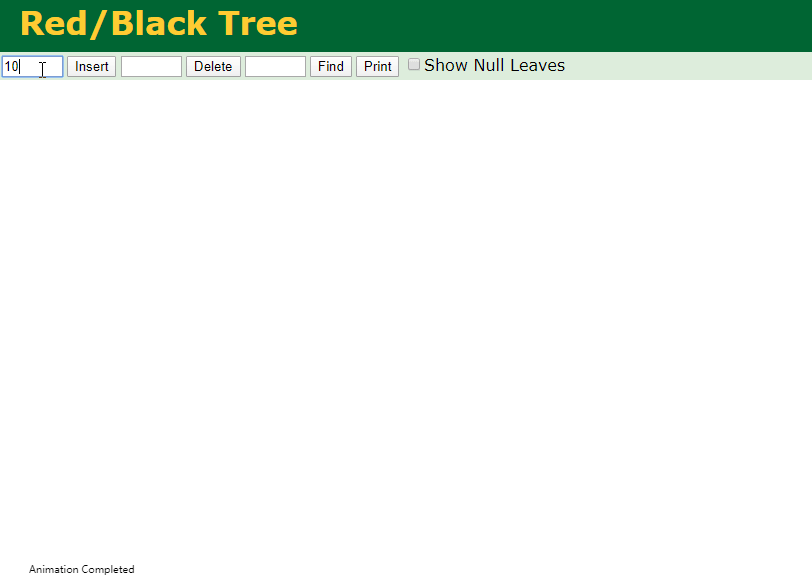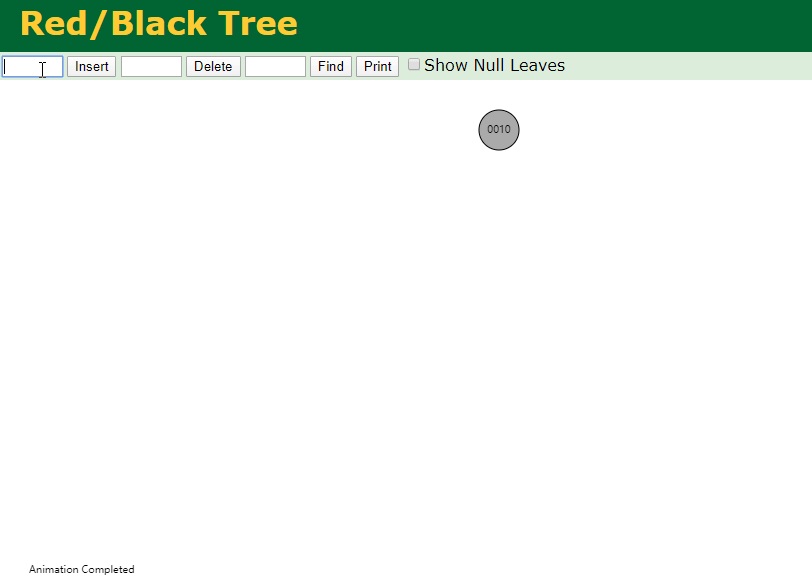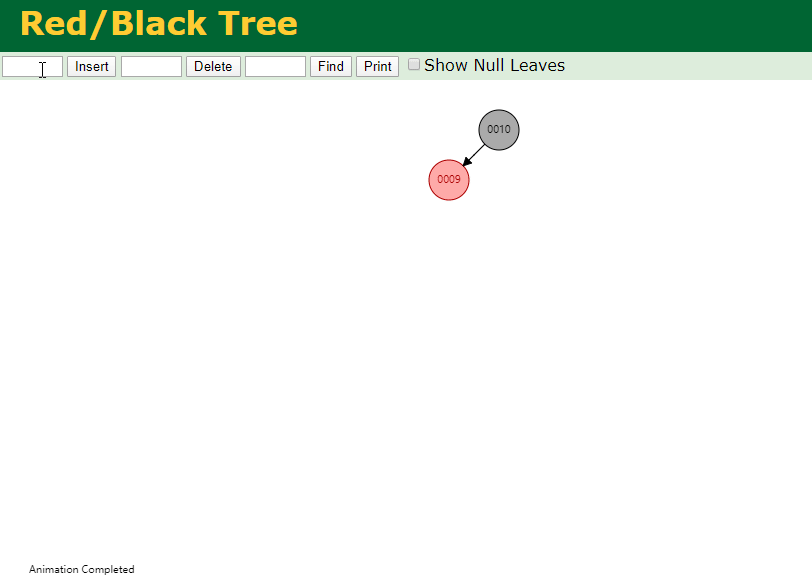
继续插入8之后，破坏了红黑树，此时需要旋转加变色了。

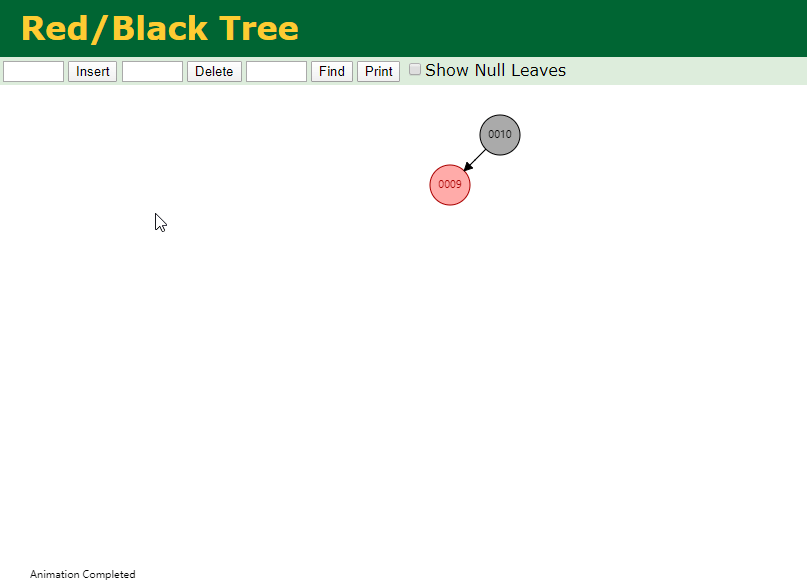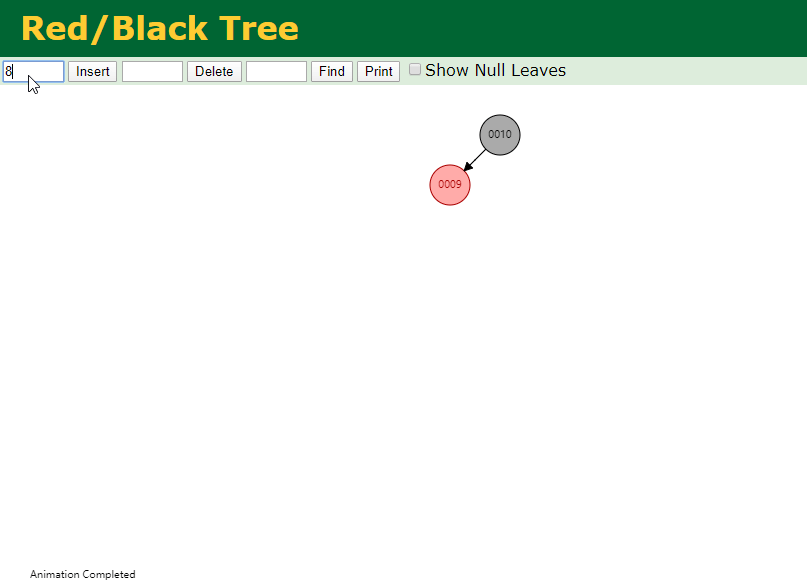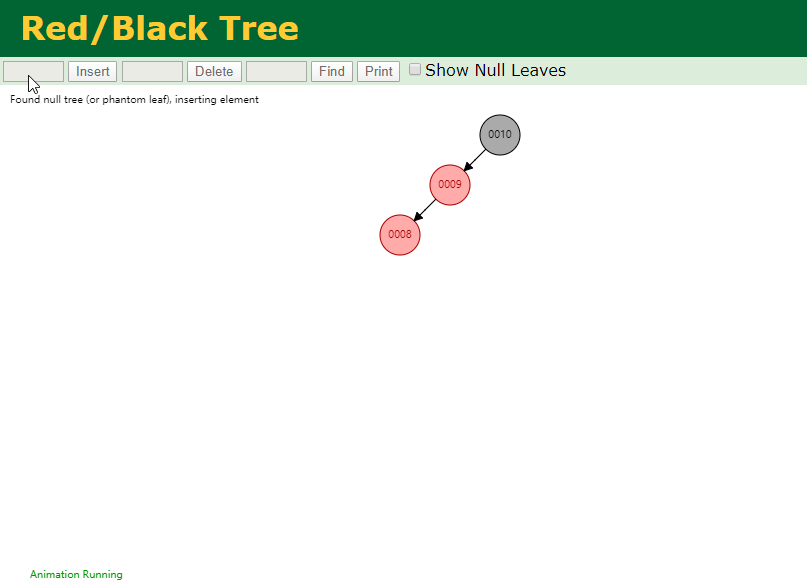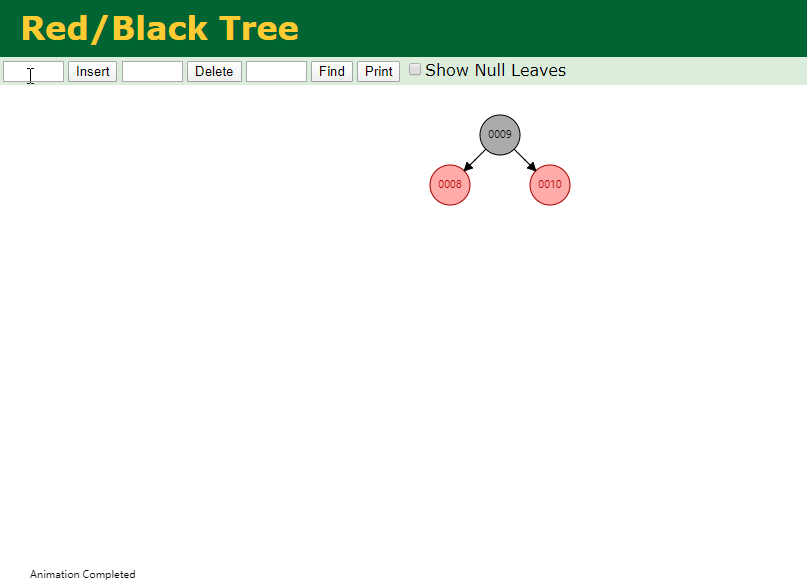
看下涉及到的具体代码

/**
* 插入结点
* @param T 红黑树的根
* @param key 插入结点值
* @description 找到位置,初始化结点，插入结点,调整红黑树
*/
void RBTree_Insert(RBTRoot** T, ElemType key) {
    RBTree pre; // pre保存了上一个x位置的指针(引用)
    RBTree x = (*T)->root;
    pre = x;
    while (x != (*T)->nil) {
        pre = x;
        if (x->key == key) {
            printf("\n%d已存在\n",key);
            return;
        } else if (key < x->key)
            x = x->lchild;
        else
            x = x->rchild;
    }

    // 初始化插入结点,将结点设为红色
    x = (RBTree) malloc(sizeof(RBNode));
    x->key = key;
    x->lchild = x->rchild = (*T)->nil;
    x->color = RED;
    x->parent = pre;

    // 根节点引用没有发生变化，
    // 插入根节点，直接插入,否则,向保存x父结点的pre左孩子或者右孩子插入x
    if ((*T)->root == (*T)->nil)
        (*T)->root = x;
    else if (key < pre->key)
        pre->lchild = x;
    else
        pre->rchild = x;
    // 插入之后，进行修正处理
    RBTree_Insert_FixUp(*T, x);
}

/**
* 红黑树插入修正函数
* @param T 红黑树的根
* @param x 插入的结点
* @description 用到变色和旋转
*/
void RBTree_Insert_FixUp(RBTRoot* T, RBTree x) {
   // 当前结点的父结点为红色需调整 注：根节点 parent是指向nil
   // (1) 叔叔结点是红色: (1.1,1.2)左右分支,一样处理,变色即可
   // (2) 叔叔结点是黑色：(2.1,2.2)左分支下左右孩子 (2.3,2.4)右分支下左右孩子

   while (x->parent->color == RED) {
        // 首先父结点是祖父结点的左分支还是右分支
        if (x->parent == x->parent->parent->lchild) {
            // 判断叔叔结点颜色
            if (x->parent->parent->rchild->color == RED) {
                // 将父结点和叔叔结点改为黑色,祖父结点改为红色
                x->parent->color = BLACK;
                x->parent->parent->rchild->color = BLACK;
                x->parent->parent->color = RED;
                x = x->parent->parent;
            } else {
                // 叔叔结点的颜色为黑色:分父结点的(1)左孩子 (2)右孩子
                // (1)父结点左孩子：父结点颜色变为BLACK，祖父节点变RED，右旋处理
                if (x->parent->lchild == x) {
                    x->parent->color = BLACK;
                    x->parent->parent->color = RED;
                    // 注意这里是x->parent->parent 以祖父节点作为旋转的根节点
                    RBTree_R_Rotate(T, x->parent->parent);
                } else {
                // (2)右孩子,先左旋转，转为上面(1)父结点左孩子的情况
                // 借助循环下次就会运行到(1)然后右旋

                    RBTree_L_Rotate(T, x->parent);
                }
            }
        } else {
            // 祖父结点的右分支
            if (x->parent->parent->lchild->color == RED) {
                // 叔叔结点为红色,左右分支都一样处理
                x->parent->color = BLACK;
                x->parent->parent->lchild->color = BLACK;
                x->parent->parent->color = RED;
                x = x->parent->parent;
            } else {
                // 叔叔为黑色
                // 父结点的右分支
                if (x->parent->rchild == x) {
                    x->parent->color = BLACK;
                    x->parent->parent->color = RED;
                    RBTree_L_Rotate(T, x->parent->parent);  // 左旋
                } else {
                    // 父结点的左分支
                    RBTree_R_Rotate(T, x->parent);  // 右旋
                }
            }
        }
        // 每次循环结束需要将根节点涂黑,因为可能在某次变色时,根节点变为红色
        // 不可放在循环外部
        // T->root->color = BLACK;
   }
    T->root->color = BLACK;
}

void RBTree_R_Rotate(RBTRoot* T, RBTree x) {
    RBTree lc;
    lc = x->lchild;
    x->lchild = lc->rchild;
    if (lc->rchild != T->nil)
        lc->rchild->parent = x;

    lc->parent = x->parent;
    if (lc->parent == T->nil)
        T->root = lc;
    else if (x->parent->lchild == x)
        x->parent->lchild = lc;
    else if (x->parent->rchild == x)
        x->parent->rchild = lc;
    x->parent = lc;
    lc->rchild = x;
}

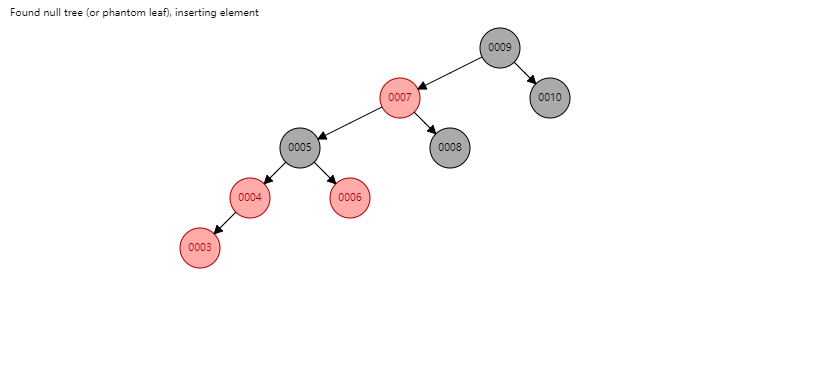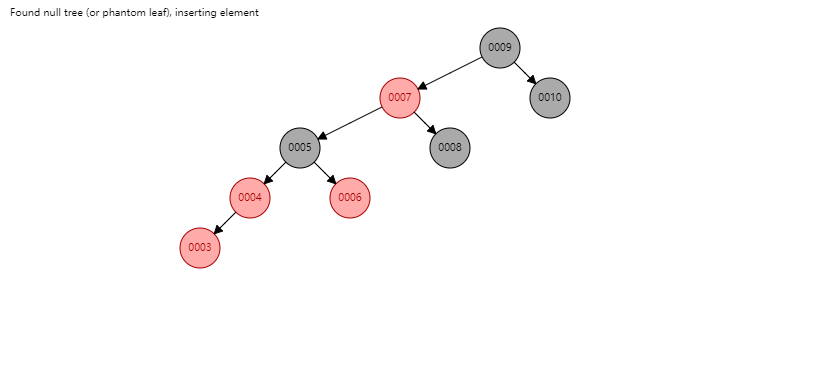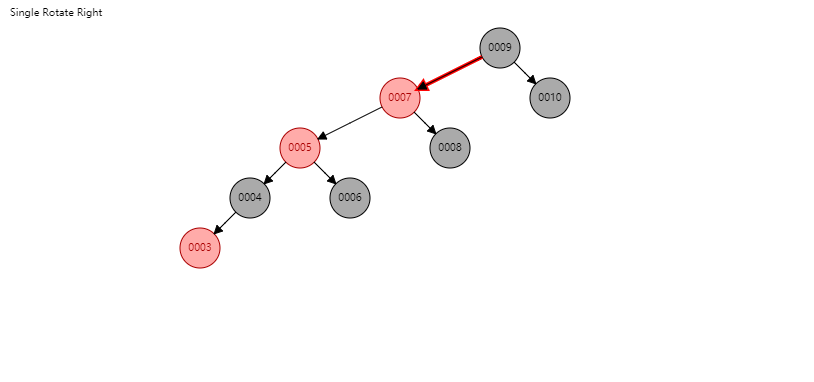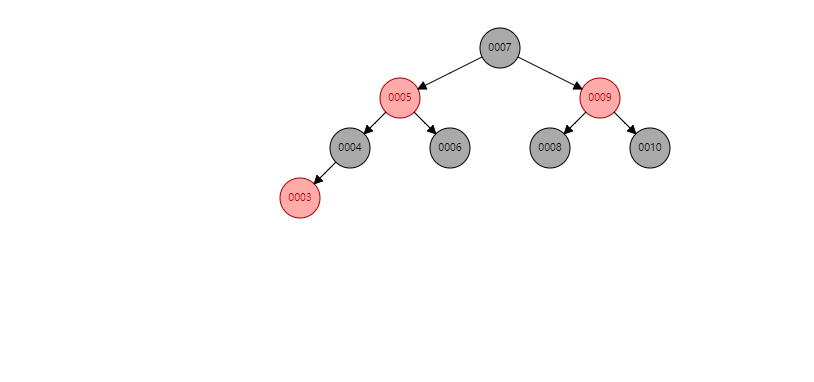
动手构建一棵红黑树，构建的过程中去代码中找构建的规律，去编写代码理解代码。接下来把剩余的结点插入。

这一个地方需要关注一下在插入3之后，眼看红黑树慢慢演变为单支树，但是由于其性质，避免了单支树的产生。这也是为什么红黑树也是一棵自平衡树。

参考

红黑树，超强动静图详解，简单易懂

posted @ 2020-10-21 16:41 Wonkey 阅读(319) 评论(0) 编辑收藏举报

刷新页面返回顶部

Stronger

I will try to be what I want to be！

红黑树-结点的插入

红黑树介绍

红黑树结点的插入

公告