【AtCoder - hhkb2020_d Simplified Reversi】 想法-棋盘问题

【AtCoder - hhkb2020_d Simplified Reversi】 想法-棋盘问题

传送门

Problem Statement

There is a grid with N rows and N columns of squares. Let (i,j) be the square at the i-th row from the top and the j-th column from the left.

Each of the central (N−2)×(N−2) squares in the grid has a black stone on it. Each of the 2N−1 squares on the bottom side and the right side has a white stone on it.

Q queries are given. We ask you to process them in order. There are two kinds of queries. Their input format and description are as follows:

• 1 x: Place a white stone on (1,x). After that, for each black stone between (1,x) and the first white stone you hit if you go down from (1,x) replace it with a white stone.
• 2 x: Place a white stone on (x,1). After that, for each black stone between (x,1) and the first white stone you hit if you go right from (x,1), replace it with a white stone.

How many black stones are there on the grid after processing all Q queries?

Constraints

• 3≤N≤2×10^5
• 0≤Q≤min(2N−4,2×10^5)
• 2≤x≤N−1
• Queries are pairwise distinct.

---

Input

Input is given from Standard Input in the following format:

N Q
Query1
⋮⋮
QueryQ

Output

Print how many black stones there are on the grid after processing all Q queries.

---

Sample Input 1 Copy

5 5
1 3
2 3
1 4
2 2
1 2

Sample Output 1 Copy

1

After each query, the grid changes in the following way:

---

Sample Input 2 Copy

200000 0

Sample Output 2 Copy

39999200004

---

Sample Input 3 Copy

176527 15
1 81279
2 22308
2 133061
1 80744
2 44603
1 170938
2 139754
2 15220
1 172794
1 159290
2 156968
1 56426
2 77429
1 97459
2 71282

Sample Output 3 Copy

31159505795

题意

一个\(n*n\)的棋盘，中心\(（n-2）*（n-2）\)的部分摆满了黑子，最后一列和最后一行摆满了白子。

现在有q个操作，每次操作从第一行（列）第x列（行）这个位置，往下（右）放白子，如果是什么都没放的位置或者已经放了黑子的位置就直接放上去 ，碰到第一颗白子就停止。问q次操作后还剩多少黑棋？

题解

首先比较显然的是一开始黑棋的数量是（n-2）*（n-2）个，每一次操作会减少一部分黑子，这个减少的数量取决于最近的白子距第一行（列）的距离。

如图，如果是一个列操作，就从它指定的第x列从上往下走，直到碰到第一颗白子为止。

如果是一个行操作就从它指定的第x行从左往右走，走到第一颗白子位置，在图上可以看到，因为刚刚先进行了一个列操作，所以再进行行操作时不能走到底，只能走到刚刚进行过列操作的那一列为止。

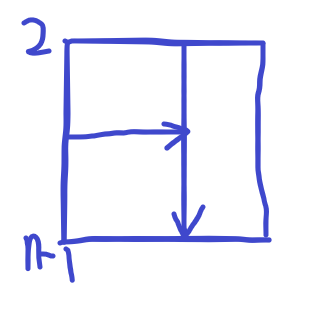
这道题解法比较巧妙，需要亿点点想法

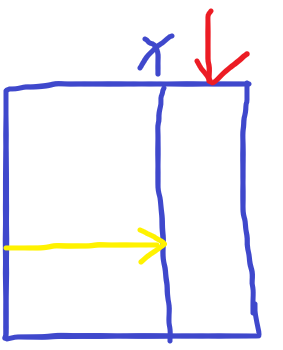
观察上面这张图可以发现，如果x这一列已经被操作过了，那么无论横向（黄色）怎么操作都无法影响到x右侧（红色）部分，如果再有x右侧的列操作，那么贡献值永远是不变的，因为红色这个区域里第一行到离它最近的白子的为止不会再发生改变了，因为x全都会帮他挡住（拒之门外）。

上面是在讨论列方向上，横方向上也是同理。

也就是说，我们维护一下横向操作的最小横坐标是w，纵向操作的最小纵坐标是h。

用数组col[i]维护如果要对第i列进行操作，离它最近的白子在哪个位置

用数组row[i]维护如果要对第i行进行操作，离它最近的白子在哪个位置

• 如果现在要进行横坐标为x的横操作
  • 如果x<w，那么把第x行到第w行的col值都更新为当前的h，因为如上图解析的那样，有了新来的x的阻隔，第x行到第w行这之间的col值不会再发生任何变化了，所以要对他们进行赋值，如果后续对他们进行了操作，就可以O(1)读取col值然后获得答案贡献值。
  • 如果x>=w，那么col[x]一定已经存在了，直接获取答案即可，这样一次操作会使黑子减少col[x]-2个，从黑子数量中减去即可

纵向操作也是同理，在此不再赘述。

Code

/****************************
* Author : W.A.R            *
* Date : 2020-11-02-21:39   *
****************************/
/*
*/
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<string>
#include<set>
#define IOS ios::sync_with_stdio(false)
#define show(x) std:: cerr << #x << " = " << x << std::endl;
#define mem(a,x) memset(a,x,sizeof(a))
#define Rint register int
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
const int maxm=2e6+10;
const ll mod=1e9+7;
namespace Fast_IO{
    const int MAXL((1 << 18) + 1);int iof, iotp;
    char ioif[MAXL], *ioiS, *ioiT, ioof[MAXL],*iooS=ioof,*iooT=ioof+MAXL-1,ioc,iost[55];
    char Getchar(){
        if (ioiS == ioiT){
            ioiS=ioif;ioiT=ioiS+fread(ioif,1,MAXL,stdin);return (ioiS == ioiT ? EOF : *ioiS++);
        }else return (*ioiS++);
    }
    void Write(){fwrite(ioof,1,iooS-ioof,stdout);iooS=ioof;}
    void Putchar(char x){*iooS++ = x;if (iooS == iooT)Write();}
    inline int read(){
        int x=0;for(iof=1,ioc=Getchar();(ioc<'0'||ioc>'9')&&ioc!=EOF;)iof=ioc=='-'?-1:1,ioc=Getchar();
		if(ioc==EOF)exit(0);
        for(x=0;ioc<='9'&&ioc>='0';ioc=Getchar())x=(x<<3)+(x<<1)+(ioc^48);return x*iof;
    }
    inline long long read_ll(){
        long long x=0;for(iof=1,ioc=Getchar();(ioc<'0'||ioc>'9')&&ioc!=EOF;)iof=ioc=='-'?-1:1,ioc=Getchar();
		if(ioc==EOF)exit(0);
        for(x=0;ioc<='9'&&ioc>='0';ioc=Getchar())x=(x<<3)+(x<<1)+(ioc^48);return x*iof;
    }
    template <class Int>void Print(Int x, char ch = '\0'){
        if(!x)Putchar('0');if(x<0)Putchar('-'),x=-x;while(x)iost[++iotp]=x%10+'0',x/=10;
        while(iotp)Putchar(iost[iotp--]);if (ch)Putchar(ch);
    }
    void Getstr(char *s, int &l){
        for(ioc=Getchar();ioc==' '||ioc=='\n'||ioc=='\t';)ioc=Getchar();
		if(ioc==EOF)exit(0);
        for(l=0;!(ioc==' '||ioc=='\n'||ioc=='\t'||ioc==EOF);ioc=Getchar())s[l++]=ioc;s[l] = 0;
    }
    void Putstr(const char *s){for(int i=0,n=strlen(s);i<n;++i)Putchar(s[i]);}
}
using namespace Fast_IO;

int main(){
	ll n=read_ll(),k=read_ll();
	vector<ll>row(n+1,n),col(n+1,n);
	ll w=n,h=n;
	ll black=(n-2)*(n-2);
	while(k--){
		ll op=read_ll(),x=read_ll();
		if(op==1){
			if(x<w){
				for(int i=x;i<=w;i++)col[i]=h;
				w=x;
			}
			black-=(col[x]-2);
		}
		else{
			if(x<h){
				for(int i=x;i<=h;i++)row[i]=w;
				h=x;
			}
			black-=(row[x]-2);
		}
	}
	printf("%lld\n",black);
	return 0;
}