排序图解:js排序算法实现

之前写过js实现数组去重, 今天继续研究数组: 排序算法实现。 排序是数据结构主要内容,并不限于语言主要在于思想;大学曾经用C语言研究过一段时间的排序实现, 这段时间有空用JS再将排序知识点熟悉一遍。
理解排序不得不提的是日本人实现的一个排序动画站, 该站对于研究排序大有益处。当然本文的排序算法并不与其一致, 本文是9种js排序实现的实践与完善: 理解其9种算法然后使每种算法代码均能正常运行。
1.插入排序
最普通的排序算法, 从数组下标1开始每增1项排序一次,越往后遍历次数越多;
原理图:
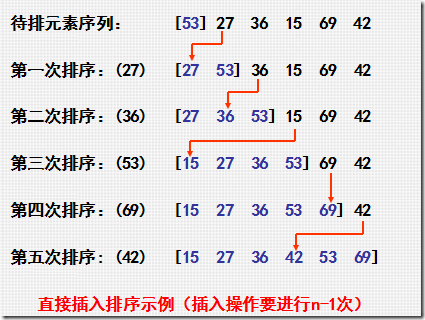
代码:
// 插入排序 从下标1开始每增1项排序一次,越往后遍历次数越多 function sort1(array) { var len = array.length, i, j, tmp, result; // 设置数组副本 result = array.slice(0); for(i=1; i < len; i++){ tmp = result[i]; j = i - 1; while(j>=0 && tmp < result[j]){ result[j+1] = result[j]; j--; } result[j+1] = tmp; } return result; }
2.二分插入排序
插入排序的一种优化实现, 通过二分法减少遍历时间。
原理图:

代码:
// 先在有序区通过二分查找的方法找到移动元素的起始位置, // 然后通过这个起始位置将后面所有的元素后移 function sort2(array) { var len = array.length, i, j, tmp, low, high, mid, result; // 赋予数组副本 result = array.slice(0); for(i = 1; i < len; i++){ tmp = result[i]; low = 0; high = i - 1; while(low <= high){ mid = parseInt((low + high)/2, 10); if(tmp < result[mid]) high = mid - 1; else low = mid + 1; } for(j = i - 1; j >= high+1; j--){ result[j+1] = result[j]; } result[j+1] = tmp; } return result; }
3.希尔排序
其排序思路有点复杂, 需花多点时间理解;排序思路:先将整个待排序记录序列分割成若干个子序列,在序列内分别进行直接插入排序,待整个序列基本有序时,再对全体记录进行一次直接插入排序。
原理图:

代码:
// 希尔排序:先将整个待排序记录序列分割成若干个子序列 // 在序列内分别进行直接插入排序,待整个序列基本有序时, // 再对全体记录进行一次直接插入排序 function sort3(array){ var len = array.length, gap = parseInt(len/2), i, j, tmp, result; // 复制数组 result = array.slice(0); while(gap > 0){ for(i = gap; i < len; i++){ tmp = result[i]; j = i - gap; while(j>=0 && tmp < result[j]){ result[j + gap] = result[j]; j = j - gap; } result[j + gap] = tmp; } gap = parseInt(gap/2); } return result; }
4.冒泡排序
很常见很容易理解的排序算法, 排序思路:遍历数组,每次遍历就将最大(或最小)值推至最前。越往后遍历查询次数越少, 跟插入排序刚好相反。
原理图:
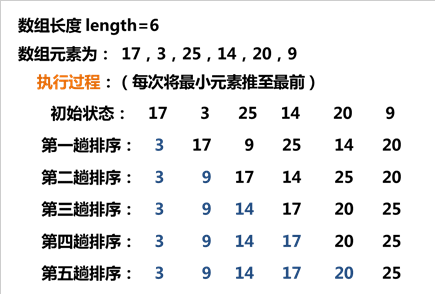
代码:
// 冒泡排序 每次将最小元素推至最前 function sort4(array) { var len = array.length, i, j, tmp, result; result = array.slice(0); for (i = 0; i < len; i++) { for (j = len - 1; j > i; j--) { if (result[j] < result[j - 1]) { tmp = result[j - 1]; result[j - 1] = result[j]; result[j] = tmp; } } } return result; }
5.改进冒泡排序
对上述冒泡排序的一种优化, 优化思路:当一次遍历前后数组不产生变化时,说明该数组已经有序,结束排序。
原理图:
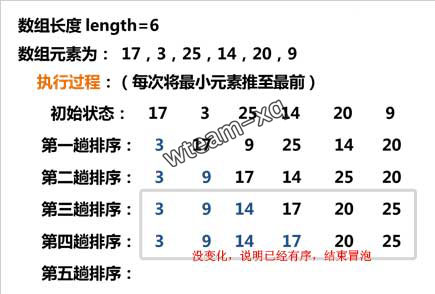
代码:
// 如果在某次的排序中没有出现交换的情况, // 那么说明在无序的元素现在已经是有序了,就可以直接返回了。 function sort5(array) { var len = array.length, i, j, tmp, exchange, result; result = array.slice(0); for (i = 0; i < len; i++) { exchange = 0; for (j = len - 1; j > i; j--) { if (result[j] < result[j - 1]) { tmp = result[j]; result[j] = result[j - 1]; result[j - 1] = tmp; exchange = 1; } } if (!exchange) return result; } return result; }
6.快速排序
快速排序在诸多算法排序中可能不是最好的, 但个人认为在JS语言实现中是最快的!以前公司项目中对比过二分插入排序、优化冒泡排序、快速排序的JS实现执行时间,几千条数据的数组在firefox下快速排序的速度比冒泡、插入排序快3至4秒(数组元素为复杂的对象,根据对象某一属性值排序)。阮一峰老师研究JS实现排序时曾只针对该种排序进行讲解:javascript的快速排序实现。
原理图:

代码:
//(1)在数据集之中,选择一个元素作为"基准"(pivot)。 //(2)所有小于"基准"的元素,都移到"基准"的左边;所有大于"基准"的元素,都移到"基准"的右边。 //(3)对"基准"左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。 function sort6(array) { var tmp_array = array.slice(0), result, quickSort = function(arr) { if (arr.length <= 1) { return arr; } var pivotIndex = Math.floor(arr.length / 2); var pivot = arr.splice(pivotIndex, 1)[0]; var left = []; var right = []; for (var i = 0; i < arr.length; i++){ if (arr[i] < pivot) { left.push(arr[i]); } else { right.push(arr[i]); } } return quickSort(left).concat([pivot], quickSort(right)); }; result = quickSort(tmp_array); return result; }
7.选择排序
实现思路跟冒泡排序差不多, 可以说是冒泡排序的衍生版本;
原理图:
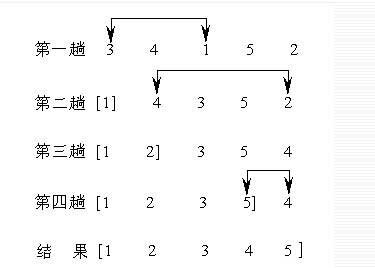
代码:
// 在无序区中选出最小的元素,然后将它和无序区的第一个元素交换位置。 // 原理跟冒泡排序一样,算是冒泡的衍生版本 function sort7(array) { var len = array.length, i, j, k, tmp, result; result = array.slice(0); for (i = 0; i < len; i++) { k = i; for (j = i + 1; j < len; j++) { if (result[j] < result[k]) k = j; } if (k != i) { tmp = result[k]; result[k] = result[i]; result[i] = tmp; } } return result; }
8.堆排序
因为js模拟二叉树比较麻烦,所以堆排序的优势用js语言无法体现, 相对而言C语言的链表在实现上更能表现堆排序,堆排序或许更适合指针类的计算机语言。本文注重图解各排序的基本思路,所以该排序的具体实现没讲太细, 如想深究实现细节请看:堆排序及其分析。
原理图:
1.调整二叉树,形成大根堆(子节点都比父节点小)。
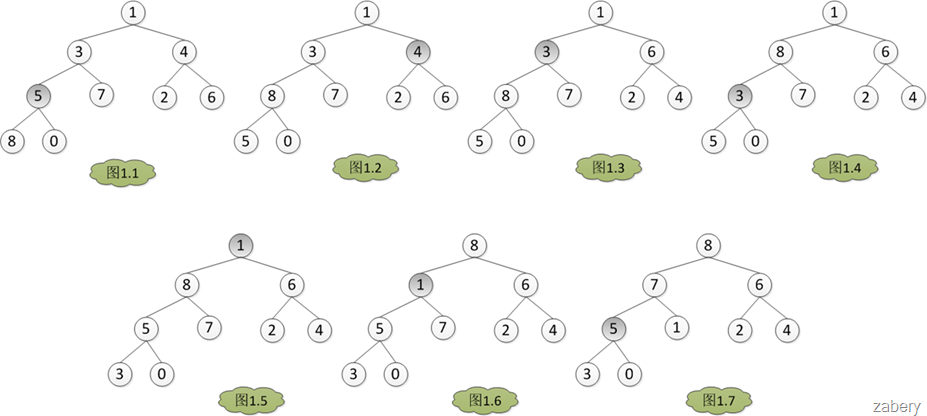
2.交换堆第一元素跟最后元素位置,最后元素弹出堆。然后继续回到1,调整堆。

3.重复2, 当所有节点弹出堆后;弹出的节点值就是有序的了。

代码:
// 1) 初始堆:将原始数组调整成大根堆的方法——筛选算法:子节点都比父节点小 // 2) 堆排序: 每次将堆顶元素与数组最后面的且没有被置换的元素互换。 // 参考代码: http://bubkoo.com/2014/01/14/sort-algorithm/heap-sort/ function sort8(array) { var result = array.slice(0); function swap(array, i, j) { var temp = array[i]; array[i] = array[j]; array[j] = temp; } function maxHeapify(array, index, heapSize) { var iMax, iLeft, iRight; while (true) { iMax = index; iLeft = 2 * index + 1; iRight = 2 * (index + 1); if (iLeft < heapSize && array[index] < array[iLeft]) { iMax = iLeft; } if (iRight < heapSize && array[iMax] < array[iRight]) { iMax = iRight; } if (iMax != index) { swap(array, iMax, index); index = iMax; } else { break; } } } function buildMaxHeap(array) { var i, iParent = Math.floor(array.length / 2) - 1; for (i = iParent; i >= 0; i--) { maxHeapify(array, i, array.length); } } function sort(array) { buildMaxHeap(array); for (var i = array.length - 1; i > 0; i--) { swap(array, 0, i); maxHeapify(array, 0, i); } return array; } return sort(result); }
9.归并排序
很容易理解且执行效率一般(js实现)的排序, 排序思路:将无序的数组 拆成N部分进行有序处理,然后合并;
原理图:

代码:
// 合并排序:将无序的数组 拆成N部分进行有序处理,然后合并; // 参考代码: https://gist.github.com/paullewis/1982121 function sort9(array) { var result = array.slice(0); // 递归调用合并函数 function sort(array) { var length = array.length, mid = Math.floor(length * 0.5), left = array.slice(0, mid), right = array.slice(mid, length); if (length === 1) { return array; } return merge(sort(left), sort(right)); } // 合并 两有序的数组 function merge(left, right) { var result = []; while (left.length || right.length) { if (left.length && right.length) { if (left[0] < right[0]) { result.push(left.shift()); } else { result.push(right.shift()); } } else if (left.length) { result.push(left.shift()); } else { result.push(right.shift()); } } return result; } return sort(result); }
本文代码及demo:
参考文章:
1.排序动画站;
2.9种js排序实现;
4.堆排序及其分析;
5.常见排序算法;



