马尔可夫毯（Markov Blanket）

马尔可夫毯（Markov Blanket）

        最近接触到马尔可夫毯（MarkovBlanket）这个概念，发现网上资料不多，通俗易懂的解释甚少，查了一些资料后，决定写一个总结。

        提到马尔可夫毯，就会有一堆从名字上看很相近的概念，比如马尔可夫链（Markov Chain, MC）、隐马尔可夫模型（Hidden Markov Model, HMM）、马尔可夫随机场（MarkovRandom Field, MRF）等等。其实，马尔可夫毯与这些概念不同，它是一个局部的概念，而不是一个整体模型级别的概念。以下内容主要参考【何宪. 基于贝叶斯网络的马尔可夫毯发现算法研究[D]. 电子科技大学, 2012.】，更多内容请参阅原文献。

        首先看马尔可夫毯的定义：

 

这种纯符号的定义看起来有些抽象，形象一点说，把一个随机变量全集U分成互斥的三部分，变量X以及集合A和B，三个子集没有交集，并集即为全集U；如果说给定集合A时，变量X与集合B没有任何关系，则称集合A为变量X的马尔可夫毯。在式(2-16)中，集合MB即为我说的集合A，{U-MB-{X}}即为我说的集合B，符号“⊥”表示“独立”，符号“|”表示在给定xx条件下，因此式(2-16)可读为“在给定集合MB时，变量X与{U-MB-{X}}独立”。

        打个比方说，全集U是整个社会，X是你个人，MB就是你生活圈子里的人。按照哲学的说法，万事万物都是有联系的；但是，你并不会与社会里的所有人有什么关系，而是通过你的生活圈子和他们有间接的关系，即当给定你的生活圈子以后，你和社会其余的人是没啥关系的（独立的）。

        特殊一点，当以上提到的全集是可信的贝叶斯网络（Bayesian Network, BN）的各个结点的时候：

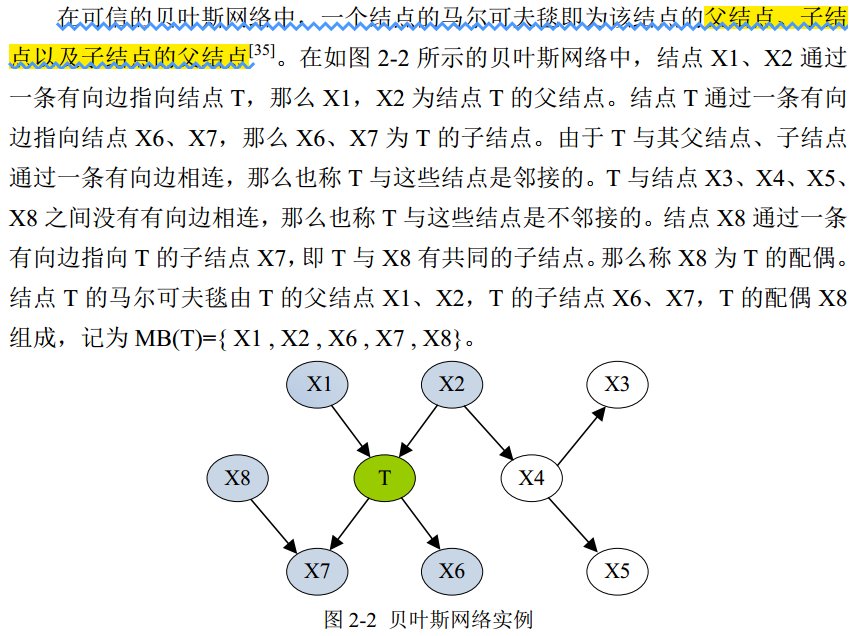
        这段话说的比较严谨，通俗点儿说就是在可信的贝叶斯网络中，一个节点的马尔可夫毯包括它的爸妈、它的所有孩子、还有它的配偶，即生它的人和它参与生出来的人及它的现任妻子（因为你会发现孩子并非都是T和配偶共有的^_^）。再通俗点儿说，其实用我国传统的家庭组成来解释最为形象，以家里的男主人为核心（即图中的T），一家人包括爷爷奶奶（X1、X2，即T的爸妈）、小俩口（T他自己、X8）、孩子（X6、X7，其中X7是小俩口一起生的，X6是T和前妻生的，但现归T抚养，已经没前妻啥事儿了^_^）。值得注意的是，每个节点的配偶可以不止一个（即允许一夫多妻制，假如添加一条从X4到X6的箭头，则X4也是T的配偶），也可以没有配偶（即单身，比如图中的X4，虽然有两个孩子，但目前单身），当然我在这里假设的性别也是随时在变的，找谁的马尔可夫毯，谁就是男性^_^

        那么马尔可夫毯有什么用处呢？文中提到了特征选择（当然这只是用处之一）：

        换句话说，一个人的马尔可夫毯就是和你有关系的所有人（按式2-16定义）。如果想要调查这个人，总不能把全社会的所有人都调查一下吧（大量的特征冗余），其实只要找出这个人的马尔可夫毯人群调查一下就好了（特征选择）。特别地，如果这个社会是贝叶斯网络，马尔可夫毯人群只包括自己的家人，相当于人只与自己的家人有关系，和其他人没关系，是一种简化的模型，具体可以查一查贝叶斯网络的概念。

        那么怎么找出这个人的马尔可夫毯人群呢？那就去看看原文献吧……

        最后简单谈一点贝叶斯网络，它是一个有向无环图（Directed Acyclic Graph, DAG），如图2-2所示，结点之间的连结都是有向箭头，且不能沿着箭头走一圈。贝叶斯网络是马尔可夫链的推广，马尔可夫链限定了结构只能是一条链，而贝叶斯网络则不再限定结构是一个链，但二者都遵守马尔可夫假设，即一个结点只依赖于它的上一个节点（一阶马尔可夫假设）。有关马尔可夫链、隐马尔可夫模型、贝叶斯网络可以看一看《数学之美》，“统计语言模型”一章会涉及到马尔可夫链，专门有一章叫“隐含马尔可夫模型”，还有一章叫“马尔可夫链的扩展——贝叶斯网络”，讲的比较通俗易懂，此处不再赘述。

        文中几次提到了可信的贝叶斯网络，在文献第3章给了可信性的定义：

        也不知道上面的定义是不是指的“可信的贝叶斯网络”中的“可信”，个人理解“可信的”意思可能是指这个贝叶斯网络是个真正的贝叶斯网络，即满足马尔可夫假设。

来源：CSDN
原文：https://blog.csdn.net/jbb0523/article/details/78424522