用R分析时间序列(time series)数据

时间序列（time series）是一系列有序的数据。通常是等时间间隔的采样数据。如果不是等间隔，则一般会标注每个数据点的时间刻度。

time series data mining 主要包括decompose（分析数据的各个成分，例如趋势，周期性），prediction（预测未来的值），classification（对有序数据序列的feature提取与分类），clustering（相似数列聚类）等。

这篇文章主要讨论prediction（forecast，预测）问题。 即已知历史的数据，如何准确预测未来的数据。

 

 下面以time series 普遍使用的数据 airline passenger为例。 这是十一年的每月乘客数量，单位是千人次。

原始数据（passenger.csv）：

112 115 145 171 196 204 242 284 315 340 360 417
118 126 150 180 196 188 233 277 301 318 342 391
132 141 178 193 236 235 267 317 356 362 406 419
129 135 163 181 235 227 269 313 348 348 396 461
121 125 172 183 229 234 270 318 355 363 420 472
135 149 178 218 243 264 315 374 422 435 472 535
148 170 199 230 264 302 364 413 465 491 548 622
148 170 199 242 272 293 347 405 467 505 559 606
136 158 184 209 237 259 312 355 404 404 463 508
119 133 162 191 211 229 274 306 347 359 407 461
104 114 146 172 180 203 237 271 305 310 362 390
118 140 166 194 201 229 278 306 336 337 405 432

 

如果想尝试其他的数据集，可以访问这里：  https://datamarket.com/data/list/?q=provider:tsdl

可以很明显的看出，airline passenger的数据是很有规律的。

 

先从简单的方法说起。给定一个时间序列，要预测下一个的值是多少，最简单的思路是什么呢？

（1）mean（平均值）：未来值是历史值的平均。

 

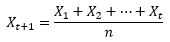
（2）exponential smoothing （指数衰减）：当去平均值得时候，每个历史点的权值可以不一样。最自然的就是越近的点赋予越大的权重。

或者，更方便的写法，用变量头上加个尖角表示估计值

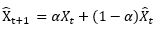
（3) snaive ： 假设已知数据的周期，那么就用前一个周期对应的时刻作为下一个周期对应时刻的预测值

（4） drift：飘移，即用最后一个点的值加上数据的平均趋势

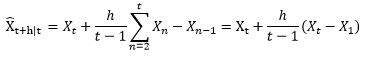
介绍完最简单的算法，下面开始介绍两个time series里面最火的两个强大的算法： Holt-Winters 和 ARIMA。 上面简答的算法都是这两个算法的某种特例。

（5）Holt-Winters：  三阶指数平滑

 Holt-Winters的思想是把数据分解成三个成分：平均水平（level），趋势（trend），周期性（seasonality）。R里面一个简单的函数stl就可以把原始数据进行分解：

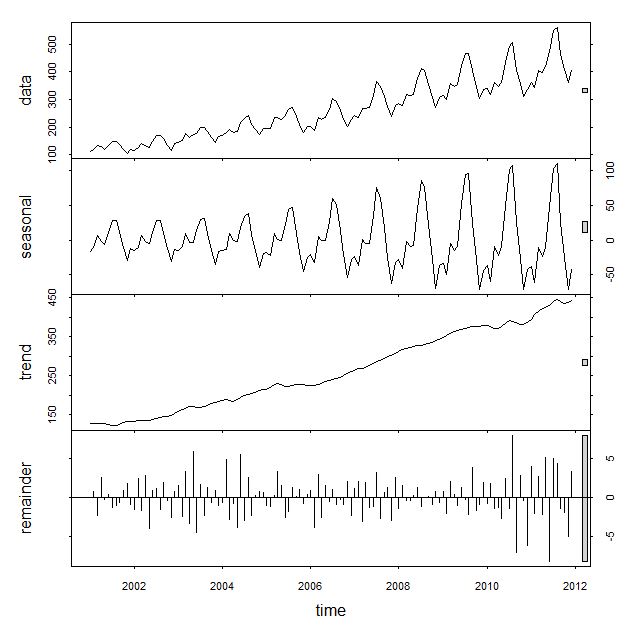
一阶Holt—Winters假设数据是stationary的（静态分布），即是普通的指数平滑。二阶算法假设数据有一个趋势，这个趋势可以是加性的(additive,线性趋势)，也可以是乘性的(multiplicative,非线性趋势)，只是公式里面一个小小的不同而已。  三阶算法在二阶的假设基础上，多了一个周期性的成分。同样这个周期性成分可以是additive和multiplicative的。 举个例子，如果每个二月的人数都比往年增加1000人，这就是additive；如果每个二月的人数都比往年增加120%，那么就是multiplicative。

 R里面有Holt-Winters的实现，现在就可以用它来试试效果了。我用前十年的数据去预测最后一年的数据。 性能衡量采用的是RMSE。 当然也可以采用别的metrics：

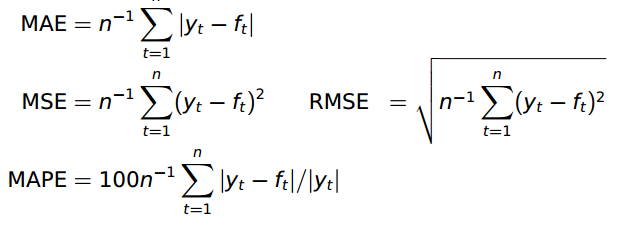
预测结果如下：

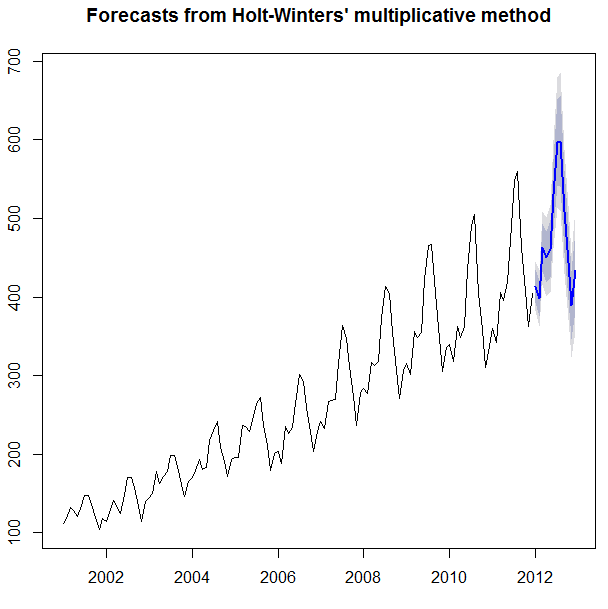
结果还是很不错的。

（6） ARIMA： AutoRegressive Integrated Moving Average

ARIMA是两个算法的结合：AR和MA。其公式如下：

是白噪声，均值为0， C是常数。  ARIMA的前半部分就是Autoregressive：， 后半部分是moving average： 。  AR实际上就是一个无限脉冲响应滤波器（infinite impulse resopnse）, MA是一个有限脉冲响应（finite impulse resopnse），输入是白噪声。

ARIMA里面的I指Integrated（差分）。 ARIMA（p,d,q）就表示p阶AR，d次差分，q阶MA。  为什么要进行差分呢？ ARIMA的前提是数据是stationary的，也就是说统计特性（mean，variance，correlation等）不会随着时间窗口的不同而变化。用数学表示就是联合分布相同：

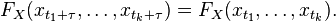
当然很多时候并不符合这个要求，例如这里的airline passenger数据。有很多方式对原始数据进行变换可以使之stationary：

（1） 差分，即Integrated。 例如一阶差分是把原数列每一项减去前一项的值。二阶差分是一阶差分基础上再来一次差分。这是最推荐的做法

（2）先用某种函数大致拟合原始数据，再用ARIMA处理剩余量。例如，先用一条直线拟合airline passenger的趋势，于是原始数据就变成了每个数据点离这条直线的偏移。再用ARIMA去拟合这些偏移量。

（3）对原始数据取log或者开根号。这对variance不是常数的很有效。

如何看数据是不是stationary呢？这里就要用到两个很常用的量了： ACF（auto correlation function）和PACF(patial auto correlation function)。对于non-stationary的数据，ACF图不会趋向于0，或者趋向0的速度很慢。 下面是三张ACF图，分别对应原始数据，一阶差分原始数据，去除周期性的一阶差分数据：

acf(train)
acf(diff(train,lag=1))
acf(diff(diff(train,lag=7)))

 

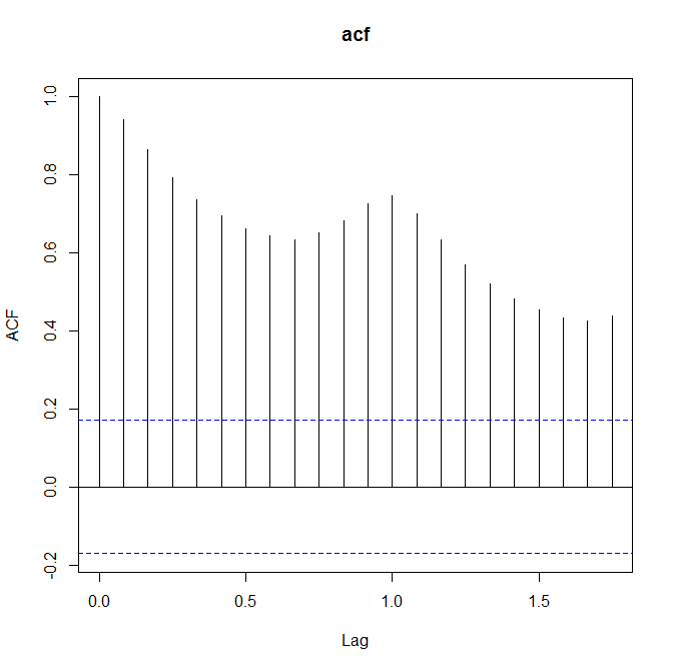
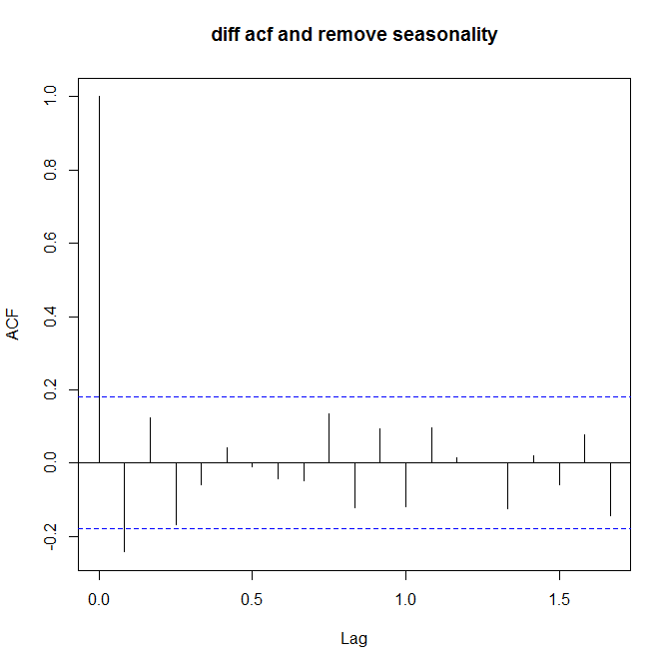
确保stationary之后，下面就要确定p和q的值了。定这两个值还是要看ACF和PACF：

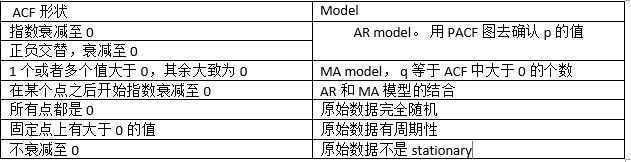
确定好p和q之后，就可以调用R里面的arime函数了。 以上是ARIMA的基本概念，要深究它的话还是有很多内容要补充的。 ARIMA更多表示为  ARIMA(p,d,q)(P,D,Q)[m] 的形式，其中m指周期（例如7表示按周），p,d,q就是前面提的内容，P,D,Q是在周期性方面对应的p,d,q含义。

值得一提的是，R里面有两个很强大的函数： ets 和 auto.arima。 用户什么都不需要做，这两个函数会自动挑选一个最恰当的算法去分析数据。

在R中各个算法的效果如下：

代码如下：

passenger = read.csv('passenger.csv',header=F,sep=' ')
p<-unlist(passenger)

#把数据变成time series。  frequency=12表示以月份为单位的time series. start 表示时间开始点，可以用c(a,b,...)表示，  例如按月为单位，标准的做法是 start=c(2011,1) 表示从2011年1月开始
#如果要表示按天的，建议用 ts(p,frequency=7,start=c(1,1))  很多人喜欢用 ts(p,frequency=365,start=(2011,1))但是这样有个坏处就是没有按星期对齐
pt<-ts(p,frequency=12,start=2001) #
plot(pt)
train<-window(pt,start=2001,end=2011+11/12)
test<-window(pt,start=2012)

library(forecast)
pred_meanf<-meanf(train,h=12)
rmse(test,pred_meanf$mean) #226.2657

pred_naive<-naive(train,h=12)
rmse(pred_naive$mean,test)#102.9765

pred_snaive<-snaive(train,h=12)
rmse(pred_snaive$mean,test)#50.70832

pred_rwf<-rwf(train,h=12, drift=T)
rmse(pred_rwf$mean,test)#92.66636

pred_ses <- ses(train,h=12,initial='simple',alpha=0.2)
rmse(pred_ses$mean,test) #89.77035

pred_holt<-holt(train,h=12,damped=F,initial="simple",beta=0.65)
rmse(pred_holt$mean,test)#76.86677  without beta=0.65 it would be 84.41239

pred_hw<-hw(train,h=12,seasonal='multiplicative')
rmse(pred_hw$mean,test)#16.36156

fit<-ets(train)
accuracy(predict(fit,12),test) #24.390252


pred_stlf<-stlf(train)
rmse(pred_stlf$mean,test)#22.07215

plot(stl(train,s.window="periodic"))  #Seasonal Decomposition of Time Series by Loess

fit<-auto.arima(train)
accuracy(forecast(fit,h=12),test) #23.538735

ma = arima(train, order = c(0, 1, 3),   seasonal=list(order=c(0,1,3), period=12))
p<-predict(ma,12)
accuracy(p$pred,test)  #18.55567
BT = Box.test(ma$residuals, lag=30, type = "Ljung-Box", fitdf=2)

 

看到有人问代码中的rmse是怎么写的，其实‘accuracy()’ 函数已经包含了各种评价指标了。这里贴上自己写的代码：

wape = function(pred,test)
{ 
        len<-length(pred) 
    errSum<-sum(abs(pred[1:len]-test[1:len])) 
    corSum<-sum(test[1:len])
    result<-errSum/corSum
    result
}


mae = function(pred,test)
{ 
    errSum<-mean(abs(pred-test))    #注意  和wape的实现相比是不是简化了很多
    errSum
}

rmse = function(pred,test)
{ 
    res<- sqrt(mean((pred-test)^2) )
    res
}