数据缩放方法总结

数据缩放（Data Scaling）是数据预处理的一种重要方法，用于将不同取值范围的特征值调整到统一的范围，从而提高机器学习模型的性能和稳定性。本文将总结常见的数据缩放方法，并分析它们的优缺点及适用场景。

1. 均值归一化（Mean Normalization）：将数据缩放到[-1,1]的范围内，使数据的均值为0。具体计算方法为：$x_{scaled} = \frac{x - \text{mean}(x)}{\text{max}(x) - \text{min}(x)}$。即：

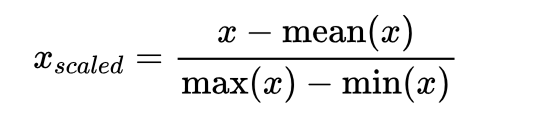
均值归一化除了将数据缩放到一个固定范围内，还能保持数据的分布形态。

2. 方差归一化（Standardization）：通过将数据缩放到均值为0，方差为1的范围内，消除不同特征之间的量纲问题。具体计算方法为：$x_{scaled} = \frac{x - \text{mean}(x)}{\text{std}(x)}$。

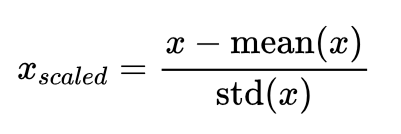
方差归一化将所有特征值分布在均值附近，使得数据具有相似的尺度。

3. 最大最小归一化（Min-Max Scaling）：将数据缩放到[0,1]的范围内。具体计算方法为：$x_{scaled} = \frac{x - \text{min}(x)}{\text{max}(x) - \text{min}(x)}$。

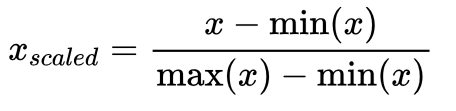
最大最小归一化保留了原始数据的分布形态和相对关系。

4. 归一化（Normalization）：将每个样本的特征向量缩放到单位范数（长度为1）。Normalization主要思想是对每个样本计算其p-范数，然后对该样本中每个元素除以该范数，这样处理的结果是是的每个处理后样本的p-范数（L1-norm, L2-norm）等于1。 具体计算方法为：$\mathbf{x} _{scaled} = \left ( \frac{x_i}{\left \| \mathbf{x} \right \|_p } \right ) _{i\in[1,n]}$。

归一化使得样本的特征向量具有统一的长度，可以消除不同特征之间的重要性差异。

5. 对数变换（Log Transformation）：通过对数据取对数，使得数据具有更均匀的分布。对数变换适用于数据具有指数增长或衰减的情况，可以使得数据更符合线性模型的要求。

6. 幂变换（Power Transformation）：通过对数据进行幂次变换，改变数据的分布形态。常用的幂次变换包括平方根、立方根、平方和倒数等。

7. 区间缩放（Interval Scaling）：将数据缩放到指定的区间内。具体计算方法为：$x_{scaled} = a + \frac{(x - \min(x))(b - a)}{\max(x) - \min(x)}$，其中$a$和$b$为目标区间的上下限。

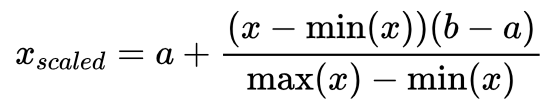
区间缩放是一种非线性变换方法，可以将数据分布到指定的区间范围内。

 

这些数据缩放方法各有优缺点，适用于不同的场景和数据类型。均值归一化和方差归一化广泛用于特征工程中，使得特征具有统一的尺度，提高机器学习模型的性能和稳定性。最大最小归一化适用于特征值分布在较小的范围内的情况，保留了原始数据的相对关系。归一化适用于需要统一特征向量长度的情况，如聚类和相似度计算。对数变换和幂变换适用于数据有偏分布的情况，能够改善数据的分布形态。而区间缩放适用于将数据缩放到指定范围内的情况。

在选择数据缩放方法时，需要根据数据的分布形态、特征的取值范围、算法模型的要求等因素综合考虑。对于不同的数据集和任务，可能需要尝试多种数据缩放方法并进行交叉验证，以选择最适合的方法。此外，需要注意在数据缩放过程中，要避免信息的损失和过拟合的问题。

综上所述，数据缩放是数据预处理的重要环节，可以提高机器学习模型的性能和稳定性。不同的数据缩放方法具有不同的优缺点和适用场景，在实际应用中需要根据具体情况选择合适的方法。