2021寒假集训——数论初步

1.28 数论初步

讲师：姚嘉宸（i207m）

质数

1.整除、质数（素数）、合数的定义。注：1既不是质数也不是合数

2.唯一分解定理&标准分解式

3.素数计数函数：小于或等于x的素数个数，称为π(x)，随着x增大，有：

\[π(x)\approx \frac{x}{ln(x)} \]

4.质数判定：2~\(\sqrt{n}\)

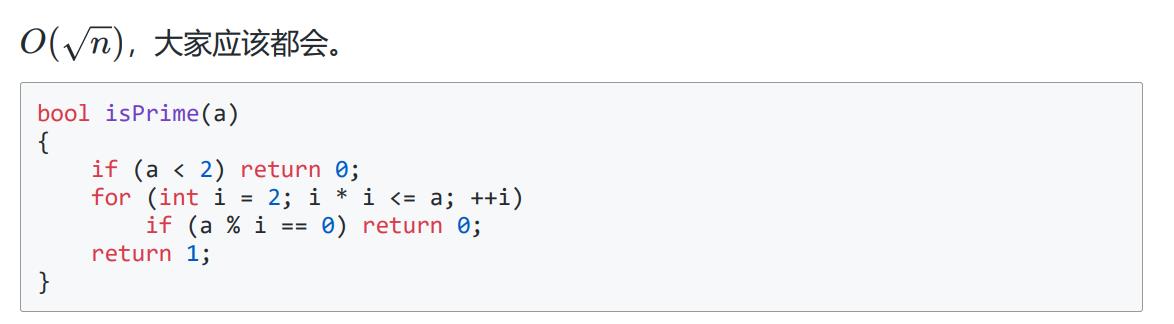
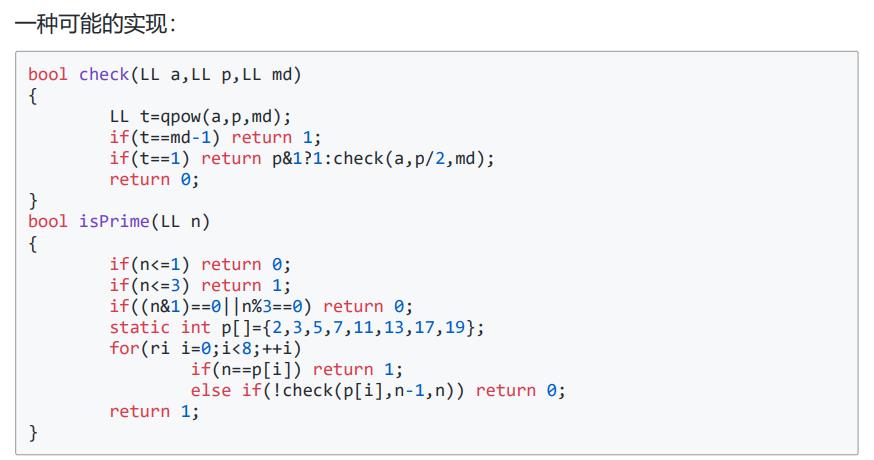
5.miller-rabin 素性测试

6.费马小定理：(不要求互素)

若a是一个整数，p是一个质数，则有

\[a^p\equiv a\space (mod\space p) \]

及证明（听不懂）

7.fermat素性测试

费马小定理逆定理不成立，使其不成立的数叫作卡迈克尔数，并且满足\(m=2^n - 1\)

8.二次探测定理

如果p是奇素数，则 \(x^2\equiv 1\space (mod\space p)\)的解为\(x=1\)或\(x=p-1\)

于是对于\(x=1\)的情况，可以“二次探测”。

*pollard-rho（生日悖论）

扩展欧几里得算法

1.欧几里得算法求gcd是log的。

\[当a>b时，有 a\% b<\frac{a}{2} \]

2.扩展欧几里得算法（exgcd）常用于求\(ax+by=gcd(a,b)\)

内容：\((a,b)=(b,a\%b)=d\)

\(\space \space \space 当b=0时，(a,0)=a，即\left\{\begin{aligned}x=1\\y=0\end{aligned}\right.\)

\(\space \space \space 当b\neq0时，由欧几里得定理可知 by+(a\space mod \space b)x=d\)

\(\space \space \space 由a \space mod\space b=a-\lfloor \frac{a}{b}\rfloor\cdot b得\)

\(\space \space \space ax+b(y-\lfloor\frac{a}{b}\rfloor\cdot x)=d\)

\(\space \space \space 即x=x，y=y-\lfloor \frac{a}{b} \rfloor \cdot x\)

递归即可

模板：

int exgcd(int a,int b,int &x,int &y){
	if(!b){x=1,y=0;return a;}
	else{
		int d=exgcd(b,a%b,y,x);
		y-=(a/b)*x;
		return d;
	}
}

P1516 青蛙的约会

剩余系求逆元

对于某个a，是否存在b，使得\(ab=1 \space(mod\space m)\)

首先考虑逆元的存在性和唯一性

存在性：当且仅当\((a,m)=1\)时有逆元。

​ 证明：考虑\(ax+my=1\)的解

唯一性：逆元若存在，一定唯一。

​ 证明：假设\(ab=ac=1(mod\space m)\)，则\(b=bac=(ba)c=c(mod\space m)\)

求逆元の5种写法

1.费马小定理

\[a\times a^{p-2}=1(mod\space p) \]

注：要求p为质数

2.exgcd

​ 求\(ax+my=1\)的解

3.线性求逆元

​ 直接放图

4.线性求逆元2 （求多个）

5.线性筛

中国剩余定理（CRT）

\[\left\{\begin{aligned}& x \equiv b_1(mod\space a_1)\\&x\equiv b_2(mod\space a_2)\\&…\\&x\equiv b_n(mod\space a_n)\end{aligned}\right. \]

其中\({a_i}\)互质，求\(x\)

有无数组解。

在\(lcm(a_i)\)的剩余系下，有唯一解：

\[x=\Sigma b_i\times M_i\times M^{-1}_i \]

其中，$$M_i= \prod_{j \ne i}a_j$$，\(M_i^{-1}\)为\(M_i\)在(mod \(a_i\))下的逆元。

扩展中国剩余定理（EXCRT）

不互质的情况

式子两两合并

P3868 裸题

欧拉函数

即\(\phi(n)\)，小于等于n的与n互质的个数

1.欧拉函数是积性函数(证明听不懂)

2.特别地，当n是奇数时，\(\phi(2n)=\phi(n)\)

3.\(n=\sum_{d|n}\phi(d)\)

4.\(\phi(p^k)=p^k-p^{k-1}\)

5.设\(n=\prod_{i=1}^{n}p_i^{k_i}\)，其中\(p_i\)是质数，则\(\phi(n)=n\prod_{i=1}^s(1-\frac{1}{p_i})\)

欧拉定理

内容：若gcd(a,m)=1，则\(a^{\phi(m)}\equiv 1(mod\space m)\)

扩展欧拉定理

内容：

\[a^b\equiv \left\{ \begin{aligned} &a^{b\space mod\space \phi(p)},&gcd(a,p)=1\\ &a^b,&gcd(a,p)\ne 1&,b<\phi(p)&(mod\space p)\\ &a^{b\space mod\space \phi(p)+\phi(p)},&gcd(a,p)\ne 1&,b\geq\phi(p) \end{aligned}\right. \]

注：扩展欧拉定理只能在指数比\(\phi(p)\)大时才能用！

P4139 《大部分人都做过》

筛法

Eratosthenes筛法

洲阁筛、Min_25筛

线性筛

线性筛φ

线性筛μ

线性筛\(\sigma_0\)

\(\sigma_0(n)\)表示\(n\)的因数个数。

设\(n=p_1^{k_1}…p_t^{k_t}\)，则\(\sigma_0(n)=\prod(k_i+1)\)

莫比乌斯反演

前置知识

引理1：

\[\forall a,b,c\in \Bbb{Z},\lfloor \frac{a}{bc}\rfloor=\lfloor \frac{\lfloor\frac{a}{b}\rfloor}{c}\rfloor \]

引理2：

\[\forall n \in \Bbb{N}_+,\lfloor\frac{n}{d}\rfloor的不同取值数\leq\lfloor2\sqrt{n}\rfloor \]

数论分块

​ 设\(k=\lfloor\frac{n}{i}\rfloor\)， 当\(\lfloor\frac{n}{j}\rfloor=k\)时，j的最大值为\(\lfloor\frac{n}{k}\rfloor\)

积性函数

eg:单位函数 恒等函数 常数函数 除数函数 欧拉函数 莫比乌斯函数

莫比乌斯函数

\[\mu(n)=\left\{\begin{aligned} &1&n=1\\&0&\exists d>1:d^2|n&\\&(-1)^{\omega(n)}&otherwise\end{aligned}\right. \]

其中\(\omega(n)\)表示n的本质不同质因子个数，也是积性函数

Dirichlet卷积

定义两个数论函数\(f,g\)的Dirichlet卷积为

\[(f*g)(n)=\sum_{d|n}f(d)g(\frac{n}{d}) \]

有交换律、结合律、分配律

eg：

\[f*\epsilon=f \]

\[\epsilon=\mu * 1 \]

\[d=1*1 \]

\[\sigma=id*1 \]

\[\phi=\mu*id \]

莫比乌斯反演

设\(f(n),g(n)\)为两个数论函数。

如果有\(f(n)=\sum_{d|n}g(d)\)，那么有\(g(n)=\sum _{d|n}\mu(d)f(\frac{n}{d})\)。

如果有\(f(n)=\sum_{n|d}g(d)\)，那么有\(g(n)=\sum _{n|d}\mu(\frac{d}{n})f(d)\)。

证明不会