强化学习实战:自定义Gym环境之扫雷
开始之前
先考虑几个问题:
- Q1:如何展开无雷区?
- Q2:如何计算格子的提示数?
- Q3:如何表示扫雷游戏的状态?
- Q4:如何设置环境中的奖励?
A1:可以使用递归函数,或是堆栈。
A2:一般的做法是,需要打开某格子时,再去统计周围的雷数。如果有方便的二维卷积函数可以调用,这会是个更简洁的方法:
$$\begin{bmatrix}
1 & 0 & 0 & 1 & 0\\
0 & 1 & 0 & 0 & 1\\
1 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 1
\end{bmatrix}\bigstar
\begin{bmatrix}
1 & 1 & 1\\
1 & 0 & 1\\
1 & 1 & 1
\end{bmatrix}=
\begin{bmatrix}
1 & 2 & 2 & 1 & 2\\
3 & 3 & 3 & 3 & 1\\
1 & 3 & 1 & 2 & 1\\
2 & 3 & 2 & 2 & 1\\
1 & 0 & 1 & 1 & 0
\end{bmatrix}$$
不妨用 $\bigstar$ 表示二维卷积运算。等号左边的5×5矩阵表示了雷的分布情况,值1表示有雷,值0表示无雷;等号左边的3×3矩阵是求解周围雷数的卷积核(或称滤波器,特征提取器);等号右边的矩阵即是所有格子的周围雷数。
代码实现起来也非常简单:
from scipy import signal import numpy as np state_mine = np.array([[1,0,0,1,0],[0,1,0,0,1],[1,0,1,0,0],[0,0,0,0,0],[0,1,0,0,1]]) KERNAL = np.array([[1,1,1],[1,0,1],[1,1,1]]) state_num = signal.convolve2d(state_mine, KERNAL, 'same')
A3:对于玩家来说,游戏状态是不完全观测的,也即需要区分观测状态和环境状态。环境状态包括雷分布矩阵,和提示数矩阵(也即上式提到的);观测状态是玩家部分可见的环境状态,需要根据格子的打开状态对雷分布矩阵进行部分屏蔽。观测状态不包括雷分布矩阵,因为一旦触雷即游戏结束,所以游戏中所有非终止状态都是无雷的。
那么对于一个大小为$M \times N$的扫雷游戏,环境状态可以表示为 $M \times N \times 2$ 的张量:频道1是雷分布矩阵,频道2是提示数矩阵;观测状态可以表示为 $M \times N \times 2$ 的张量:频道1是表示格子打开状态的矩阵(值1为打开,值0为未打开),并以此矩阵对 提示数矩阵 进行元素乘,完成对环境状态的部分屏蔽,作为第二个频道。对于numpy.array而言,元素乘是容易的:
observe_num = state_num * state_open
以下图的游戏状态为例说明:
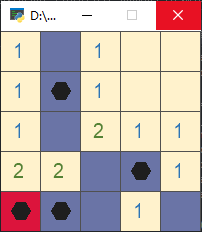
环境状态为:
$$\begin{bmatrix}
& & & & \\
& 1 & & & \\
& & & & \\
& & & 1 & \\
1 & 1 & & &
\end{bmatrix}\times
\begin{bmatrix}
1 & 1 & 1 & 0 & 0\\
1 & 0 & 1 & 0 & 0\\
1 & 1 & 2 & 1 & 1\\
2 & 2 & 2 & 0 & 1\\
1 & 1 & 2 & 1 & 1
\end{bmatrix}$$
观测状态为:
$$\begin{bmatrix}
1 & 0 & 1 & 0 & 0\\
1 & 0 & 1 & 0 & 0\\
1 & 0 & 2 & 1 & 1\\
2 & 2 & 0 & 0 & 1\\
1 & 0 & 0 & 1 & 0
\end{bmatrix}\times
\begin{bmatrix}
1 & & 1 & 1 & 1\\
1 & & 1 & 1 & 1\\
1 & & 1 & 1 & 1\\
1 & 1 & & & 1\\
1 & & & 1 &
\end{bmatrix}$$
但这种表示方式不是唯一的,比如我们可以把提示数矩阵拆成9个频道,分别表示0~8的提示数。那么观测状态就变成了 $M \times N \times 10$ 的张量(这种只有0或1的表达方式也被称为one-hot编码):
$$\begin{bmatrix}
& & & 1 & 1\\
& & & 1 & 1\\
& & & & \\
& & & & \\
& & & &
\end{bmatrix}\times
\begin{bmatrix}
1 & & 1 & & \\
1 & & 1 & & \\
1 & & & 1 & 1\\
& & & & 1\\
& & & 1 &
\end{bmatrix}\times
\begin{bmatrix}
& & & & \\
& & & & \\
& & 1 & & \\
1 & 1 & & & \\
& & & &
\end{bmatrix}\times
\begin{bmatrix}
& & & & \\
& & & & \\
& & & & \\
& & & & \\
& & & &
\end{bmatrix}\times
\cdots \times
\begin{bmatrix}
& & & & \\
& & & & \\
& & & & \\
& & & & \\
& & & &
\end{bmatrix}\times
\begin{bmatrix}
1 & & 1 & 1 & 1\\
1 & & 1 & 1 & 1\\
1 & & 1 & 1 & 1\\
1 & 1 & & & 1\\
1 & & & 1 &
\end{bmatrix}$$
状态空间的设计是灵活的,唯一的评价的标准是完整的学习系统的性能表现。如果采用以上多频道式的状态空间设计,那么后续可以很方便地使用卷积神经网络开展学习任务。你也可以把张量阵展成一维的向量,然后用全连接神经网络处理。本文后续的实现将采用 $M \times N \times 2$ 的状态空间表达。
A4:最简单的做法,无疑是通关给一个正的分,失败则给一个负的分,但这样做是否合理呢?我们知道,扫雷的通关率和雷的密度有关,对于经典的微软扫雷高级局,一个算法能有30%的通关率就已经算不错了。可以想象,在强化学习中,一个还未经过训练的模型,几乎不可能通关并拿到正的奖励分,这样会导致几乎所有的 Q(s,a) 值都是负的。大量案例说明,最终呈现出泾渭分明、有正有负的Q值,是更有效的(通过引入baseline,或设置合理的奖励)。因此,我们设计如下的奖励:
$$R = R_{step} + R_{end}$$
$R_{end}$ 表示终局的奖励:
$$R_{end} = \begin{cases}
10 & \text{ if } 游戏通关 \\
-10 & \text{ if } 游戏失败 \\
\end{cases}$$
其中 $R_{step}$ 表示每一步的奖励:
$$R_{step} = \begin{cases}
1 & \text{ if } 翻开的是已知的非雷方块 \\
1.5 & \text{ if } 翻开的是未知的非雷方块 \\
\end{cases}$$
我们为翻开未知非雷方块设置更高的奖励分,区别于已知的非雷方块,是因为翻开已知的非雷方块对游戏的胜利没有推动作用,这类似于按照最低概率翻开的贪心算法,一个很好的例子在论文 MINESWEEPER, #MINESWEEPER 的第11页。
想要知道一个方块是否是雷,我们可以直接去求解每一个方块有雷的概率,通过求解约束满足问题(CSP)来得到,这是穷举法的一种实现方式,但有时是非常耗时且耗内存的,比如你不巧地翻出了类似这样没有展开无雷区的情况:
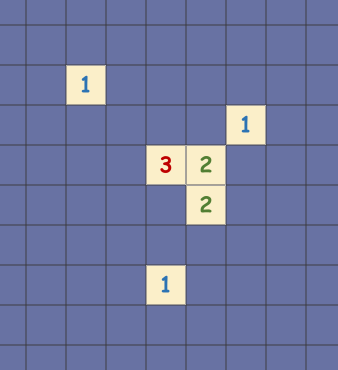
如果我们用组合数的方式列举全部情况,那么情况数是:$C_{8}^{1}×C_{7}^{1}×C_{6}^{3}×C_{5}^{2}×C_{6}^{2}×C_{8}^{1}=1344000$,要遍历完这些情况数是很费劲的,如果每一个step都运行一下CSP求解器,无疑会增加很多代码时间。
一个讨巧的方法是,只考虑每一个提示数方块的局部,而不考虑其与周围区域的耦合。对于一个提示数为 $N$ 的方块,若其周围3×3范围内的未翻开方块数是 $N_{unopened}$,未知的方块数为 $N_{unknown}$,未翻但已知有雷的方块数是 $N_{m}$,未翻但已知无雷的方块数是 $N_{mfree}$, 那么其周围的未知方块有雷的概率是:
$$\frac{N - N_{m}}{N_{unknown}}=\frac{N-N_{m}}{N_{unopened}-N_m-N_{mfree}}$$
并且我们可以得到推论:
- 若$N - N_{mine}$ = 0,则所有未知方块都是无雷的;
- 若$N=N_{unopened}-N_{mfree}$,则所有未知方块都是有雷的。
这其实也是我们玩扫雷的一种“排除法”的逻辑:先考虑局部的情况,给确定的方块标注上“有雷”或“无雷”的标签,再依据此去查看周围的区域。写成算法就是:重复地遍历所有带提示数的方块,通过以上的推论为确定的方块打上标签。之所有强调要重复地执行,是因为实际上在遍历的过程中,由于不断地引入了 $N_{m}$ 和 $N_{mfree}$ 的信息,信息从局部渐渐地扩散到了所有连通的区域,自然地完成了耦合。虽然这种做法没有求解CSP精准,但胜在速度快。实现方面,我们构建一个叫 elimination 的 numpy.array 以储存标签信息,再构建一个函数 updata_elimination 去更新它,我们可以重复地遍历3次:
self.elimination = None # 排除法确定有雷(value=1)/无雷(value=-1)/其他(value=0) ...... def update_elimination(self): self.elimination = np.zeros((self.ROW, self.COL)) iterNum = 3 while iterNum: iterNum -= 1 for i in range(self.ROW): for j in range(self.COL): if self.state_num[i,j] > 0 and self.state_open[i,j] == 1: rounds = self.getRoundSet(i, j) N = self.state_num[i,j] N_mine = 0 N_minefree = 0 N_unopened = 0 unknown_list = [] for one in rounds: if self.state_open[one] == 0: # 未翻开的方块 N_unopened += 1 if self.elimination[one] == -1: # 未翻且已知无雷的方块 N_minefree += 1 if self.elimination[one] == 1: # 未翻且已知有雷的方块 N_mine += 1 if self.elimination[one] == 0: # 未翻开且未知的方块 unknown_list.append(one) if N - N_mine == 0: # 全部未知方块都是无雷的 for one in unknown_list: self.elimination[one] = -1 if N == N_unopened - N_minefree: # 全部未知方块都是有雷的 for one in unknown_list: self.elimination[one] = 1 print(self.elimination)
文件操作和整体代码实现
步骤1:新建文件
为了运行pytorch,我使用anaconda的环境管理操作创建了名为pytorch1.1的环境名,并在这个环境下安装了openAI gym,因此我来到目录:D:\Anaconda\envs\pytorch1.1\Lib\site-packages\gym\envs\user 下,新建文件 __init__.py 和 MineSweeper_env.py。
步骤2:编写文件 MineSweeper_env.py
核心的内容在开始之前中已经进行了分析,这里就不再赘述了。一个标准的gym env类包含三个方法:reset(),step(action),和render()。
- reset() 用于初始化环境;
- step(action) 有四个返回值:state,reward,done,和info,因此我们需要在该函数中完成扫雷游戏的全部逻辑;
- render() 用于可视化环境。我在网上没有找到gym的原生方法rendering可以显示文字的说法(如果有知晓的朋友请留言,感谢!),所以是通过pyglet + 动态变量名的方式实现大量字符的显示,具体做法可见 强化学习实战 | 自定义Gym环境之显示字符串。
MineSweeper_env.py 的整体代码如下:

import gym import random import time import numpy as np from scipy import signal # 二维卷积 import pyglet # 显示文字 from gym.envs.classic_control import rendering class DrawText: # 用于在rendering中显示文字 def __init__(self, label:pyglet.text.Label): self.label=label def render(self): self.label.draw() class MineSweeperEnv(gym.Env): def __init__(self): self.MINE_NUM = 15 self.ROW, self.COL = 12, 12 self.SIZE = 40 WIDTH = self.COL * self.SIZE HEIGHT = self.ROW * self.SIZE self.viewer = rendering.Viewer(WIDTH, HEIGHT) self.state_mine = None self.state_num = None self.state_open = None self.observe_state = None self.elimination = False # 排除法确定有雷(value=1)/无雷(value=-1)/其他(value=0) self.gameOver = False def reset(self): # 初始化:布雷状态 MINE_NUM = self.MINE_NUM self.state_mine = np.zeros(self.ROW * self.COL) self.state_mine[:MINE_NUM] = 1 random.shuffle(self.state_mine) self.state_mine = self.state_mine.reshape(self.ROW, self.COL) # 初始化:提示数字 KERNAL = np.array([[1,1,1], [1,0,1], [1,1,1]]) self.state_num = signal.convolve2d(self.state_mine, KERNAL, 'same') # 初始化:打开状态 self.state_open = np.zeros((self.ROW, self.COL)) # 初始化:观测状态 observe_num = self.state_num * self.state_open self.observe_state = np.array([observe_num, self.state_open]) # 初始化:排除法状态 self.elimination = np.zeros((self.ROW, self.COL)) # 初始化:游戏是否结束 self.gameOver = False return self.observe_state def getRoundSet(self, x, y): roundSet = [] for i in range(x-1, x+2): for j in range(y-1, y+2): if 0 <= i < self.ROW and 0 <= j < self.COL and (i, j) != (x, y): roundSet.append((i, j)) return roundSet def update_elimination(self): self.elimination = np.zeros((self.ROW, self.COL)) iterNum = 3 while iterNum: iterNum -= 1 for i in range(self.ROW): for j in range(self.COL): if self.state_num[i,j] > 0 and self.state_open[i,j] == 1: rounds = self.getRoundSet(i, j) N = self.state_num[i,j] N_mine = 0 N_minefree = 0 N_unopened = 0 unknown_list = [] for one in rounds: if self.state_open[one] == 0: # 未翻开的方块 N_unopened += 1 if self.elimination[one] == -1: # 未翻且已知无雷的方块 N_minefree += 1 if self.elimination[one] == 1: # 未翻且已知有雷的方块 N_mine += 1 if self.elimination[one] == 0: # 未翻开且未知的方块 unknown_list.append(one) if N - N_mine == 0: # 全部未知方块都是无雷的 for one in unknown_list: self.elimination[one] = -1 if N == N_unopened - N_minefree: # 全部未知方块都是有雷的 for one in unknown_list: self.elimination[one] = 1 print(self.elimination) def step(self, action): # 执行动作 # action = 0~143 x, y = action//self.ROW, action%self.COL # 若打开数字不为0 if self.state_num[x, y] >= 1: self.state_open[x, y] = 1 # 若打开数字为0 则展开无雷区 if self.state_num[x, y] == 0: stack = [] stack.append((x, y)) while len(stack): row, col = stack.pop() self.state_open[row, col] = 1 for one in self.getRoundSet(row, col): # 排除已经打开的格子 if self.state_open[one] == 1: continue if self.state_num[one] >= 1: self.state_open[one] = 1 else: stack.append(one) # 是否获胜或失败/获得奖励 done, reward = False, 0 R_step, R_end = 0, 0 # 若打开已知的非雷方块 if self.elimination[x,y] == -1: R_step = 1 elif self.elimination[x,y] == 0 and self.state_mine[x,y] == 0: R_step = 1.5 # 若打开雷 则游戏失败 if self.state_mine[x, y] == 1: self.state_open[x, y] = 1 self.gameOver = True done, R_end = True, -10 # 若剩余未打开的格子数 = 雷数 则获胜 if self.ROW*self.COL - self.state_open.sum() == self.MINE_NUM: self.gameOver = True done, R_end = True, 10 reward = R_step + R_end # 报告(维持gym step的标准格式) info = {} # 观测状态 observe_num = self.state_num * self.state_open self.observe_state = np.array([observe_num, self.state_open]) return self.observe_state, reward, done, info def render(self, mode='human'): ROW, COL, SIZE = self.ROW, self.COL, self.SIZE # 画方块 for i in range(ROW): for j in range(COL): X, Y = j*SIZE, (ROW-i-1)*SIZE tile = rendering.make_polygon([(X,Y), (X+SIZE,Y), (X+SIZE,Y+SIZE), (X,Y+SIZE)], filled=True) if self.state_open[i,j] == 0: tile.set_color(106/255,116/255,166/255) if self.state_open[i,j] == 1 and self.state_mine[i,j] == 0: tile.set_color(255/255,242/255,204/255) if self.state_open[i,j] == 1 and self.state_mine[i,j] == 1: tile.set_color(220/255,20/255,60/255) self.viewer.add_geom(tile) # 画分隔线 WIDTH = COL*SIZE HEIGHT = ROW*SIZE for i in range(ROW+1): line = rendering.Line((0, i*SIZE), (WIDTH, i*SIZE)) line.set_color(80/255, 80/255, 80/255) self.viewer.add_geom(line) for j in range(COL+1): line = rendering.Line((j*SIZE, 0), (j*SIZE, HEIGHT)) line.set_color(80/255, 80/255, 80/255) self.viewer.add_geom(line) # 画数字 for i in range(ROW): for j in range(COL): exec('label_{}_{} = {}'.format(i, j, None)) names = locals() NUM = int(self.state_num[i,j]) COLOR = (255, 255, 255, 255) if NUM == 1: COLOR = (46, 117, 182, 255) elif NUM == 2: COLOR = (84, 130, 53, 255) elif NUM == 3: COLOR = (192, 0, 0, 255) elif NUM == 4: COLOR = (112, 48, 160, 255) elif NUM == 5: COLOR = (132, 60, 12, 255) elif NUM == 6: COLOR = (191, 144, 0, 255) elif NUM == 7: COLOR = (32, 56, 100, 255) elif NUM == 8: COLOR = (13, 13, 13, 255) names['label_' + str(i) + '_' + str(j)] = pyglet.text.Label('{}'.format(NUM), font_size=15, x=(j+0.32)*SIZE, y=(ROW-i-1+0.23)*SIZE, anchor_x='left', anchor_y='bottom', color=COLOR) label = names['label_{}_{}'.format(i, j)] label.draw() if self.state_mine[i,j] == 0 and self.state_open[i,j] == 1 and self.state_num[i,j] >= 1: self.viewer.add_geom(DrawText(label)) # 画雷 if self.gameOver == True: if self.state_mine[i,j] == 1: mine = rendering.make_circle(10, 6, filled=True) mine.set_color(30/255, 30/255, 30/255) translation = rendering.Transform(translation=((j+0.5)*SIZE, (ROW-i-1+0.5)*SIZE)) mine.add_attr(translation) self.viewer.add_geom(mine) return self.viewer.render(return_rgb_array=mode == 'rgb_array') # 测试代码:以随机策略执行动作 if __name__ == '__main__': MineSweeper = MineSweeperEnv() ROW, COL = MineSweeper.ROW, MineSweeper.COL MineSweeper.reset() MineSweeper.render() while MineSweeper.gameOver is not True: while True: action = random.choice(range(ROW*COL)) x, y = action//ROW, action%COL if MineSweeper.state_open[x, y] == 0: break MineSweeper.update_elimination() state, reward, done, info = MineSweeper.step(action) print(reward) MineSweeper.render() time.sleep(0.5)
直接运行文件,执行测试代码(以随机策略执行动作):
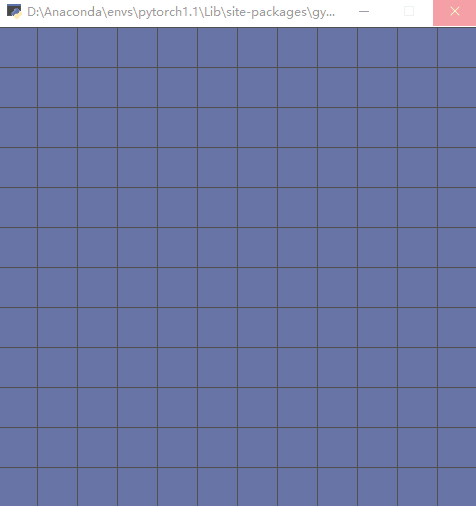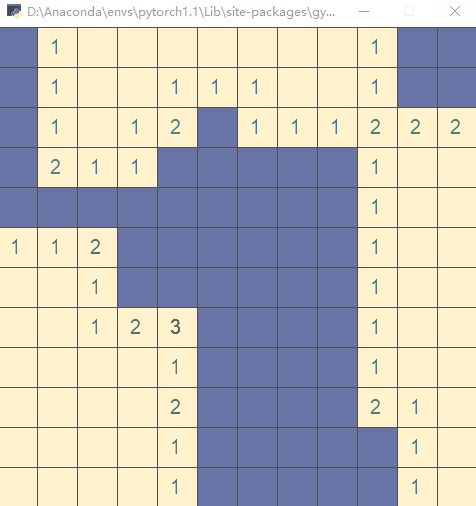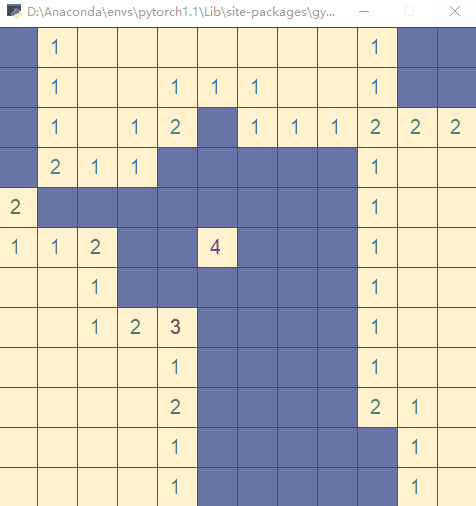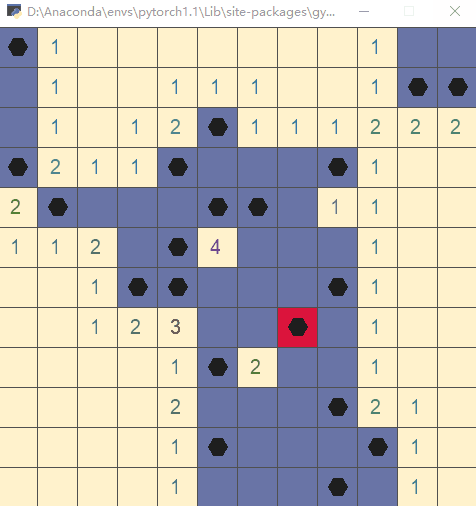
步骤3:编写 __init__.py
在 __init__.py 中引入类的信息,添加:
from gym.envs.user.MineSweeper_env import MineSweeperEnv
步骤4:注册环境
来到目录:D:\Anaconda\envs\pytorch1.1\Lib\site-packages\gym,打开 __init__.py,添加代码:
register( id="MineSweeperEnv-v0", entry_point="gym.envs.user:MineSweeperEnv", max_episode_steps=200, )
步骤5:测试环境
在相同的conda环境下,输入代码:
import gym env = gym.make('MineSweeperEnv-v0')
env.reset()
env.render()
若无报错,则说明gym环境注册成功。



