编程小实战:一类骰子游戏中的概率计算
一个骰子,一个跑道,停在某个格子上有奖励。包含这种玩法的游戏不要太多,拿“大富翁”作个图示:

在玩的时候时常在问自己:
- 我停在前方第n格的概率是多少?
- 我停在前方第n格的期望掷骰子数是多少?
- 感性上,我停在前方第100格的概率,应该和我停在前方第1000格的概率是一样的,那么这个概率是多少?
不妨就来编程解决这些疑问!
Q1:停在前方第n格的概率是多少?
不妨先考虑简单的情形:
n = 1时,至多能掷1次骰子,仅点数为1时满足条件,那么概率是 1 / 6 = 0.166667。
n = 2时,至多能掷2次骰子,点数为 (1, 1) 或 (2) 时满足条件。所有掷骰子的情况是:{ (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2) (3) (4) (5) (6) } 一共11种情况,那么概率是 2 / 11 = 0.181818。
我们可以总结出这样的公式:
- 停在前方第n格的概率 = 正好停在第n格的情况数 ÷ 给定最多投掷数的情况下,停留的位置大于等于第n格的情况数 = F(n) / G(n)
步骤1:计算F(n)
方法一:动态规划
显然,停在n格的情况数 = 停在n-1格的情况数 + 停在n-2格的情况数 + … + 停在n-6格的情况数,所以有:
- 转移方程:F(n) = F(n-1) + F(n-2) + F(n-3) + F(n-4) + F(n-5) + F(n-6)
- 边界条件:F(0) = 1,F(n<0) = 0
代码如下:
def calF(n): F_list = [0 for i in range(n+1)] for i in range(n+1): for j in range(1,7): if i - j == 0: F_list[i] += 1 # 即F(0)=1 elif i - j < 0: F_list[i] += 0 # 即F(n<0)=0 else: F_list[i] += F_list[i-j] return F_list[-1]
方法二:递归算法
动态规划与递归都有着“分而治之”的思想,在某些情况下是能相互转换的。递归算法是这么看这个问题的:于当前位置,重复地执行掷骰子这一动作。若正好停在第n格,则计数器+1,函数返回;若大于第n格,则函数返回;若小于第n格,则继续掷骰子。
代码如下:
def calF_with_RA(n, counter): # n:到目标的距离 # counter:达成条件的情况计数器 for i in range(1,7): if i == n: counter += 1 return counter elif i < n: counter = calF_with_RA(n-i, counter) return counter
步骤2:计算G(n)
如果在Step1中采用了递归算法,那么只要改写一下函数中计数器的达成条件,和函数退出的位置即可,代码如下:
def calG_with_RA(n, counter): # n:到目标的距离 # counter:达成条件的情况计数器 for i in range(1,7): if i >= n: counter += 1 else: counter = calG_with_RA(n-i, counter) return counter
步骤3:计算并画图
于是计算概率的函数有:
def calF_divide_G(n): F = calF_with_DP(n) G = calG_with_RA(n, 0) return F/G
把n=1到20的概率画出来:

if __name__ == '__main__': prob = [] for i in range(1,21): prob.append(calF_divide_G(i)) n = np.arange(1, 21).astype(dtype=np.str_) # 转换数据类型 否则plot中会显示浮点数 plt.plot(n,prob,linewidth=2,color='r',marker='o', markerfacecolor='blue',markersize=8) plt.xlabel('n') plt.ylabel('P(n)') plt.show()
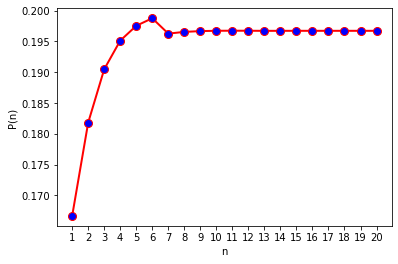
可以看出确实有收敛的趋势(n取大于25时,程序会变得异常难算,难以展示。有会数学的朋友还请指教一下要怎么证明收敛!),收敛到的概率是0.196717(保留6位小数),这也正好回答了Q3。另外,n=6时概率最大,值为0.198758(保留6位小数)。
Q2:停在前方第n格的期望掷骰子数是多少?
一个思路是,记录所有到达第n格的掷骰子“轨迹”,然后对所有轨迹进行统计。由于递归算法本身就有打印轨迹的能力,顺便再统计点相关的数据自然不在话下,于是改写递归函数:
def throw_dice(n, track, record): # n:到目标的距离 # track:骰子的轨迹 # record:记录所有轨迹的长度(即掷骰子次数) for i in range(1,7): if i == n: track.append(i) print(track) record.append(len(track)) return record elif i < n: track_ = track.copy() track_.append(i) throw_dice(n-i, track_, record) return record
遍历所有掷骰子轨迹,求出掷骰子数的概率分布和期望:
def get_dice_distribution(n): record = throw_dice(n, [], []) Min = min(record) Max = max(record) distribution = [0 for i in range(Max - Min + 1)] for num in record: distribution[num - Min] += 1 Sum = sum(distribution) for i, num in enumerate(distribution): # 求掷骰子数的概率分布 distribution[i] = num / Sum expectation = 0 # 求期望掷骰子数 for i in range(Max - Min +1): expectation += (Min + i) * distribution[i] print(expectation) return Min, Max, distribution, expectation
画出掷骰子数的概率分布(以n=10为例):

def plotDistribution(n): Min, Max, distribution, expectation = get_dice_distribution(n) N = np.arange(Min, Max+1).astype(dtype=np.str_) plt.bar(N, distribution) plt.xlabel('n') plt.ylabel('throwing times') plt.show()
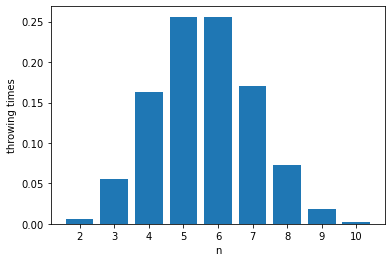
画出n=1到20的期望掷骰子数:

def plotExpectation(): expectation_list = [] for i in range(1,21): Min, Max, distribution, expectation = get_dice_distribution(i) expectation_list.append(expectation) n = np.arange(1, 21).astype(dtype=np.str_) plt.plot(n, expectation_list, linewidth=2, color='r', marker='o', markerfacecolor='blue', markersize=8) plt.xlabel('n') plt.ylabel('E(n)') plt.show() return expectation_list
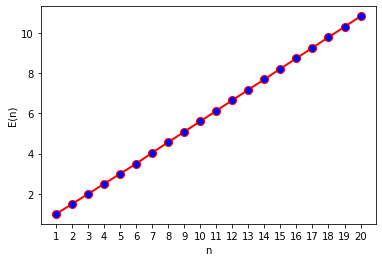
可以看出,大致上是一个线性的关系,打印出具体的数据:
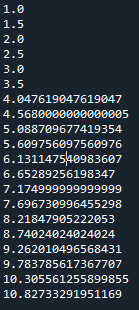
可以看出,当n小于等于6时,是线性的;大于6时,大致上是线性的。
整体代码:

import numpy as np from matplotlib import pyplot as plt def calF_with_DP(n): F_list = [0 for i in range(n+1)] for i in range(n+1): for j in range(1,7): if i - j == 0: F_list[i] += 1 # 即F(0)=1 elif i - j < 0: F_list[i] += 0 # 即F(n<0)=0 else: F_list[i] += F_list[i-j] return F_list[-1] def calF_with_RA(n, counter): # n:到目标的距离 # counter:达成条件的情况计数器 for i in range(1,7): if i == n: counter += 1 return counter elif i < n: counter = calF_with_RA(n-i, counter) return counter def calG_with_RA(n, counter): # n:到目标的距离 # counter:达成条件的情况计数器 for i in range(1,7): if i >= n: counter += 1 else: counter = calG_with_RA(n-i, counter) return counter def calF_divide_G(n): F = calF_with_RA(n, 0) G = calG_with_RA(n, 0) return F/G def plotPn(): prob = [] for i in range(1,21): prob.append(calF_divide_G(i)) n = np.arange(1, 21).astype(dtype=np.str_) # 转换数据类型 否则plot中会显示浮点数 plt.plot(n, prob, linewidth=2, color='r', marker='o', markerfacecolor='blue', markersize=8) plt.xlabel('n') plt.ylabel('P(n)') plt.show() def throw_dice(n, track, record): # n:到目标的距离 # track:骰子的轨迹 # record:记录所有轨迹的长度(即掷骰子次数) for i in range(1,7): if i == n: track.append(i) record.append(len(track)) return record elif i < n: track_ = track.copy() track_.append(i) throw_dice(n-i, track_, record) return record def get_dice_distribution(n): record = throw_dice(n, [], []) Min = min(record) Max = max(record) distribution = [0 for i in range(Max - Min + 1)] for num in record: distribution[num - Min] += 1 Sum = sum(distribution) for i, num in enumerate(distribution): # 求掷骰子数的概率分布 distribution[i] = num / Sum expectation = 0 # 求期望掷骰子数 for i in range(Max - Min +1): expectation += (Min + i) * distribution[i] print(expectation) return Min, Max, distribution, expectation def plotDistribution(n): Min, Max, distribution, expectation = get_dice_distribution(n) N = np.arange(Min, Max+1).astype(dtype=np.str_) plt.bar(N, distribution) plt.xlabel('n') plt.ylabel('throwing times') plt.show() def plotExpectation(): expectation_list = [] for i in range(1,21): Min, Max, distribution, expectation = get_dice_distribution(i) expectation_list.append(expectation) n = np.arange(1, 21).astype(dtype=np.str_) plt.plot(n, expectation_list, linewidth=2, color='r', marker='o', markerfacecolor='blue', markersize=8) plt.xlabel('n') plt.ylabel('E(n)') plt.show() return expectation_list if __name__ == '__main__': # plotPn() # plotDistribution(10) expectation_list = plotExpectation()
小结
使用动态规划和递归算法解决了问题(实际上可以完全依靠递归)。递归函数由于具有打印轨迹的能力,携带信息多,可拓展性强,稍微改写就能满足需要。



