理想的正方形（单调队列在二维的应用）

理想的正方形

 

 

题解：

用单调队列分别维护行与列。

这里只讲求 n*n 区间内的最大值的维护方法,最小值同样的方法维护即可。

具体实现方法:

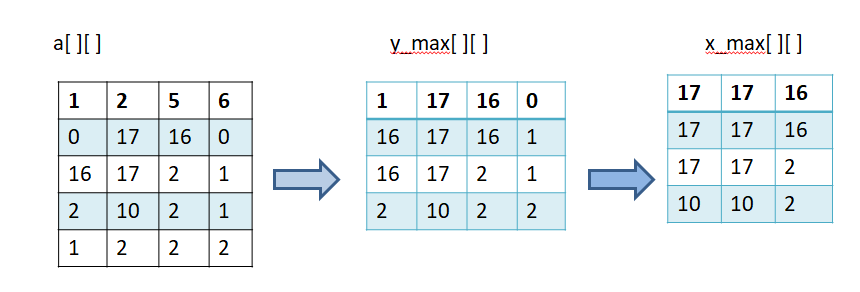
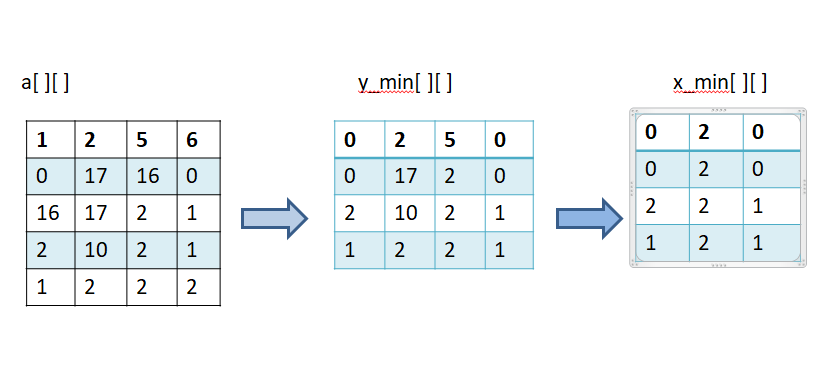
• 遍历每一行，从上到下维护每一列的每一段n长度内的最大值，得到y_max数组；
• 之后遍历y_max数组，也是遍历每一行，不过这时候要从左到右维护了，也就是行内维护，维护每一行内长度为n的区间内的最大值，得到x_max数组；
• x_max数组就是原数组从左到右，从上到下每一个n*n区间内的最大值了。

 

 

 

 

代码说明：

原数组：mat，列数组：Q；

遍历每一行，当行达到了n，就说明列向已经满足了n，这个时候就开始在行内维护n长度的最大值了（也就是说我的代码并没有完全等到y_max构造完就开始构造x_max了）

AC_Code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
const int inf = 0x3f3f3f3f;

struct Container{
    deque<int> qmin;
    deque<int> qmax;
    Container():qmin(), qmax() {}
    void push(int n){
        while( !qmin.empty() && qmin.back()>n ) qmin.pop_back();
        qmin.push_back(n);
        while( !qmax.empty() && qmax.back()<n ) qmax.pop_back();
        qmax.push_back(n);
    }
    void pop(int n){
        if( qmin.size() && qmin.front()==n ) qmin.pop_front();
        if( qmax.size() && qmax.front()==n ) qmax.pop_front();
    }
    int _max(){
        return qmax.front();
    }
    int _min(){
        return qmin.front();
    }
};

int main()
{
    int a,b,n;
    scanf("%d%d%d",&a,&b,&n);
    vector<vector<int> > mat(a,vector<int>(b));
    for(auto &v: mat){
        for(auto &i: v){
            scanf("%d",&i);
        }
    }
    vector<Container>Q(b);//列
    int ans = inf;
    for(int i=0; i<a; i++){
        if( i>=n ){                    //纵向维护
            for(int j=0;j<b;j++){
                Q[j].pop(mat[i-n][j]);//因为是单调维护,所以把mat[i-n][j]相同的值删掉就相当于把他及之前的数都给删掉了
            }
        }
        for(int j=0;j<b;j++){       //纵向维护
            Q[j].push(mat[i][j]);
        }
        if( i<n-1 ) continue;       //因为要是n*n的,所以首先要满足纵向长度达到了n
        Container C;
        for(int j=0;j<b;j++){       //横向维护
            if( j-n>=0 ){
                C.pop(Q[j-n]._max());
                C.pop(Q[j-n]._min());
            }
            C.push(Q[j]._max());
            C.push(Q[j]._min());
            if( j>=n-1 ) ans = min(ans,C._max()-C._min());
        }
    }
    printf("%d\n",ans);
    return 0;
}

 

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
const int inf = 0x3f3f3f3f;

struct node{
    int val;
    int idx;
};
deque<node>col_qmin[maxn], col_qmax[maxn], row_qmin, row_qmax;
int mat[maxn][maxn];

int main()
{
    int a,b,n;
    scanf("%d%d%d",&a,&b,&n);
    for(int i=0;i<a;i++) for(int j=0;j<b;j++) scanf("%d",&mat[i][j]);
    int ans = inf;
    for(int i=0; i<a; i++){
        if( i>=n ){
            for(int j=0;j<b;j++){
                while( col_qmin[j].size() && col_qmin[j].front().idx<=i-n ) col_qmin[j].pop_front();
                while( col_qmax[j].size() && col_qmax[j].front().idx<=i-n ) col_qmax[j].pop_front();
            }
        }
        for(int j=0;j<b;j++){
            while( col_qmin[j].size() && col_qmin[j].back().val>mat[i][j] ) col_qmin[j].pop_back();
            col_qmin[j].push_back(node{mat[i][j],i});
            while( col_qmax[j].size() && col_qmax[j].back().val<mat[i][j] ) col_qmax[j].pop_back();
            col_qmax[j].push_back(node{mat[i][j],i});
        }

        if( i<n-1 ) continue;
        row_qmin.clear(); row_qmax.clear();

        for(int j=0;j<b;j++){
            if( j>=n ){
                while( row_qmin.size() && row_qmin.front().idx<=j-n ) row_qmin.pop_front();
                while( row_qmax.size() && row_qmax.front().idx<=j-n ) row_qmax.pop_front();
            }
            while( row_qmin.size() && row_qmin.back().val>col_qmin[j].front().val ) row_qmin.pop_back();
            row_qmin.push_back(node{col_qmin[j].front().val,j});
            while( row_qmax.size() && row_qmax.back().val<col_qmax[j].front().val ) row_qmax.pop_back();
            row_qmax.push_back(node{col_qmax[j].front().val,j});

            if( j>=n-1 ){
                ans = min(ans,row_qmax.front().val-row_qmin.front().val);
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}