皇宫看守(树形dp)


题解:
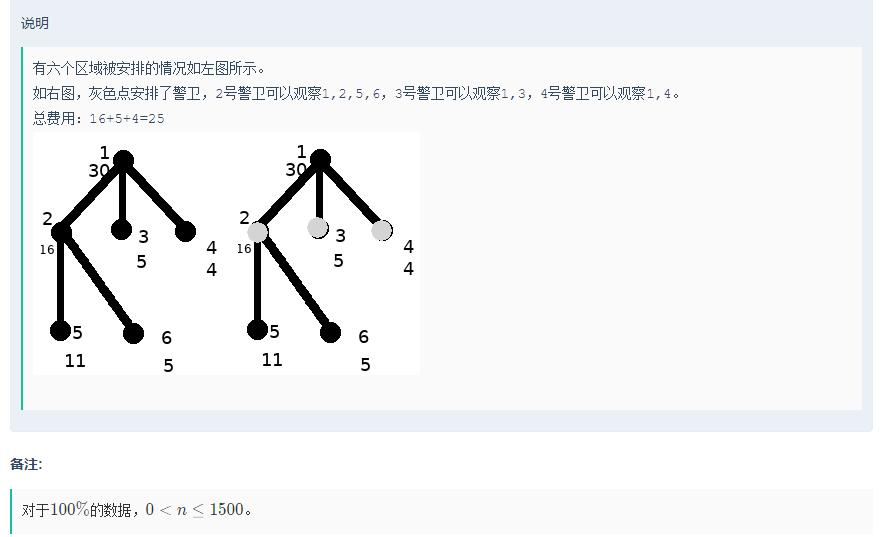
不同于战略游戏那道题要求每边有人看守,即只能靠自己或者靠儿子,本题要求每个点有人看守,即对于点root可以靠自己靠儿子或靠父亲
设dp[root][0/1/2]表示0靠自己1靠爸爸2靠儿子
root靠自己可以从儿子的三种状态转移,但是要加上自己设看守的费用
root靠爸爸可以让儿子靠自己或者靠儿子的儿子(好爸爸)
注意这里!root靠儿子必须要有一个儿子靠自己,其余儿子靠自己或者靠儿子的儿子,实现见代码
特别的,根结点不能靠爸爸,叶子结点不能靠儿子
AC_Code:
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1500+10; 5 const int mod = 1e9+7; 6 const int inf = 0x3f3f3f3f; 7 8 int cnt[maxn],dp[maxn][3], son[maxn][maxn], k[maxn],fa[maxn]; 9 int n,x; 10 11 //dp[i][0]:靠自己可以看守到i所需的最小花费 12 //dp[i][1]:靠爸爸可以看守到i所需的最小花费 13 //dp[i][2]:靠儿子可以看守到i所需的最小花费 14 15 void dfs(int root){ 16 if( !cnt[root] ){ //叶子节点 17 dp[root][0] = k[root]; 18 dp[root][1] = 0; 19 dp[root][2] = inf; 20 return ; 21 } 22 23 for(int i=1;i<=cnt[root];i++){ 24 dfs( son[root][i] ); 25 } 26 dp[root][0] = k[root]; 27 int f = 0; 28 for(int i=1;i<=cnt[root];i++){ 29 dp[root][0] += min(dp[son[root][i]][1], min(dp[son[root][i]][0], dp[son[root][i]][2])); 30 dp[root][1] += min(dp[son[root][i]][0], dp[son[root][i]][2]); 31 dp[root][2] += min(dp[son[root][i]][0], dp[son[root][i]][2]); 32 33 if( dp[son[root][i]][0]<=dp[son[root][i]][2] ){//标记有没有哪个儿子靠自己比靠儿子的花费少的 34 f = 1; 35 } 36 } 37 if( !f ){//若没有 38 int minn = 0x3f3f3f3f; 39 for(int i=1;i<=cnt[root];i++){ 40 minn = min(minn, dp[son[root][i]][0]-dp[son[root][i]][2]); 41 } 42 dp[root][2] += minn; 43 } 44 } 45 46 int main() 47 { 48 memset(dp,0,sizeof(dp)); 49 scanf("%d",&n); 50 for(int i=1;i<=n;i++){ 51 int x; scanf("%d",&x); 52 scanf("%d%d",&k[x],&cnt[x]); 53 for(int j=1;j<=cnt[x];j++){ 54 scanf("%d",&son[x][j]); 55 fa[son[x][j]] = x; 56 } 57 } 58 for(int i=1;i<=n;i++){ 59 if( !fa[i] ){ 60 dfs(i); 61 int ans = min(dp[i][0], dp[i][2]); 62 printf("%d\n",ans); 63 break; 64 } 65 } 66 return 0; 67 }
参考博客:here


