最大团入门

完全子图：对于一个给定的无向图\(G = \left ( V,E\right )\)。如果\(U\subseteq V\)，且对任意\(u，v\subseteq U\)，有\(\left ( u，v\right )\subseteq E\)，则称\(U\)就是\(G\)的完全子图

团：\(G\)的完全子图\(U\)是\(G\)的团当且仅当\(U\)不包含在\(G\)的更大的完全子图中，即\(U\)就是最大完全子图。

\(G\)的最大团是指\(G\)中所含定点数最多的团。

e.g.图来自here

 

 图a是一个无向图，图b、c、d都是图a的团，且都是最大团。

模板题：Maximum Clique（无向图最大团）

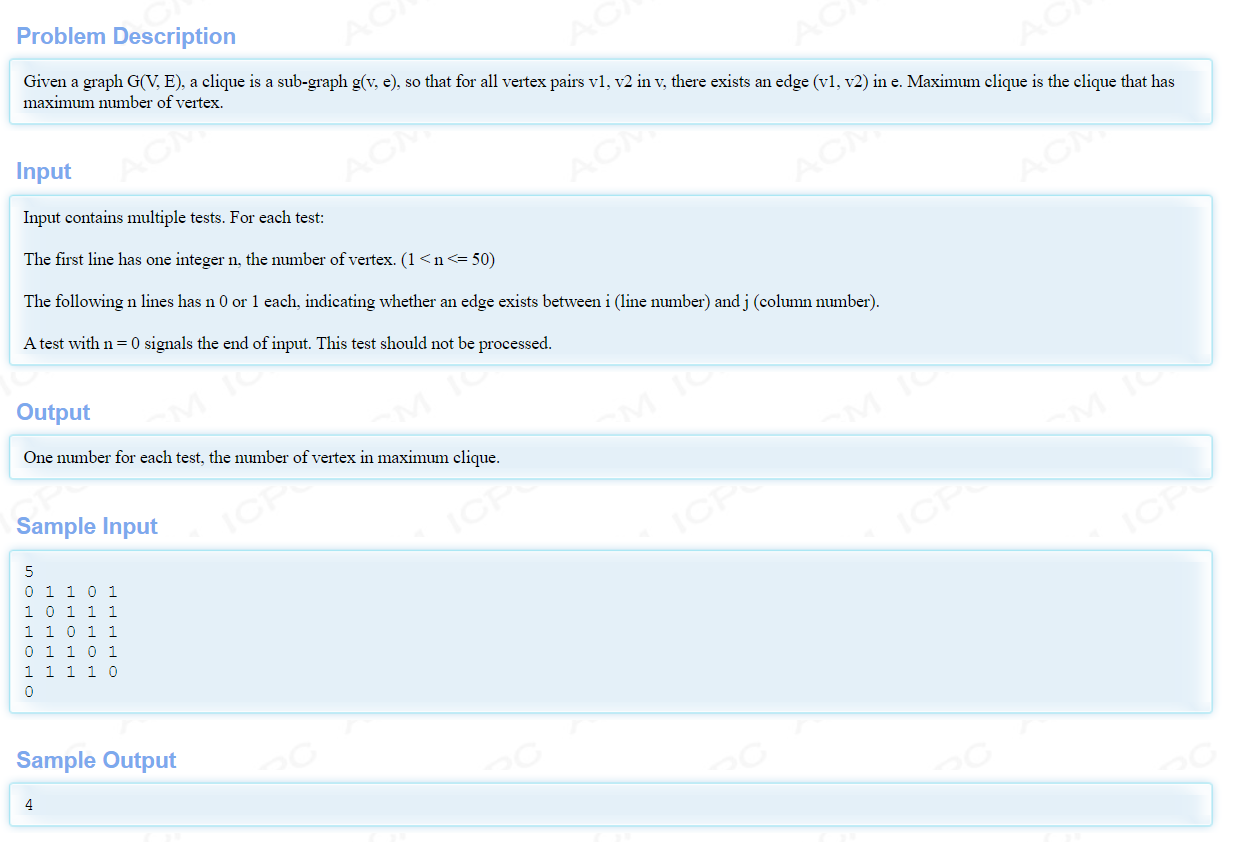
最暴力的方法：来自here

将n个点加入一个集合U1，遍历U1中的点，每次选择1个点P1作为最大团的第一个点，即DFS的第一层。

遍历U1中剩下的点，选出与P1相连的点，加入集合U2，每次选择U2中的一个点P2作为最大团的第二个点，即DFS的第二层。

遍历U2中剩下的点，选出与P2相连的点，加入集合U3，每次选择U3中的一个点P3作为最大团的第三个点，即DFS的第三层（因为团即最大完全子图，要求各个点两两相连，因此只要从之前的集合中选择点即可，只有这些点是与之前的点相连的）。

……

以此类推，到DFS的最后一层m，即此时的Um为空集时，递归结束，求出了一个团。返回上一层继续递归其他情况……选出其中的最大团输出。
 

以上是最朴素的思路，但是这样的时间复杂度太高了，所以我们考虑剪枝：

1.显然，当DFS进行到某一层x时，如果当前层数（即团内点的数量）加上集合Ux中剩下点的数量小于等于已得出的答案（即使把剩下的点全部加入团中也无法更新答案），那我们可以直接返回上一层。

2.倒序遍历，采用DP进行优化，DP[i]表示第i个及之后的点所能组成的最大团。若当前层数为x，剩下的点从i开始，那么如果 x+DP[i]<=ans ，那么同样可以直接返回。
 

以下是 只进行稍微剪枝的暴力法代码

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>

using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 60;

int G[maxn][maxn],V[maxn][maxn];
int n,ans,dp[maxn];

void dfs(int deep,int num){
    if( !num ){
        ans = deep>ans?deep:ans;//ans取最大值
        return ;
    }
    for(int i=1;i<=num;i++){
        if( deep+1+num-i<ans ) return ;//剪枝
        int cur = V[deep][i];
        if( deep+dp[cur]<ans ) return ;//优化
        int cnt = 0;
        for(int j=i+1;j<=num;j++){
            int nxt = V[deep][j];
            if( G[cur][nxt] ) V[deep+1][++cnt] = nxt;
        }
        dfs(deep+1,cnt);
    }
}

int main()
{
    while( ~scanf("%d",&n) && n){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                scanf("%d",&G[i][j]);
            }
        }
        ans = 0;
        memset(dp,0,sizeof(dp));
        for(int i=n;i>0;i--){
            int cnt = 0;
            for(int j=i+1;j<=n;j++){
                if( G[i][j] ){
                    V[1][++cnt] = j;
                }
            }
            dfs(1,cnt);
            dp[i] = ans;
        }
        cout<<ans<<endl;
    }
    return 0;
}