选择（dp）

选择

 

 

 

 题解：

 

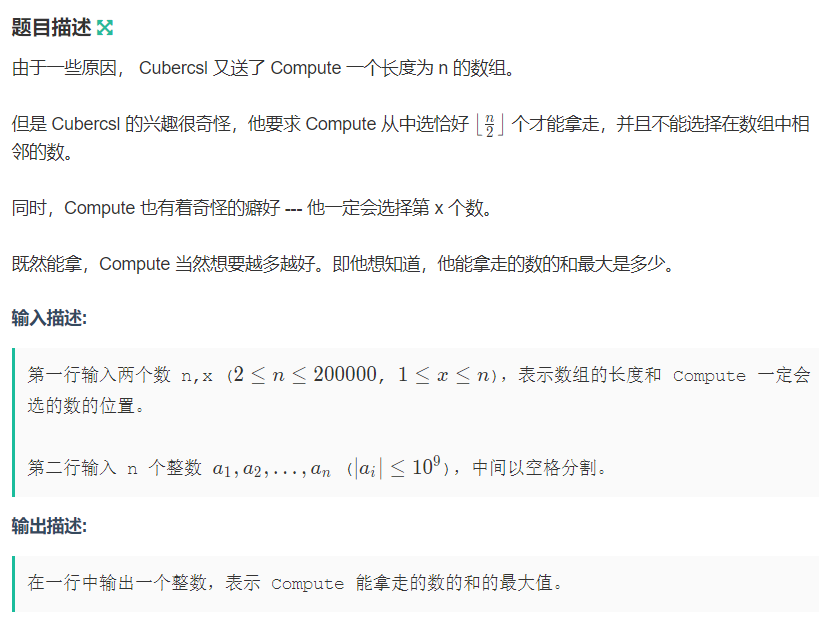
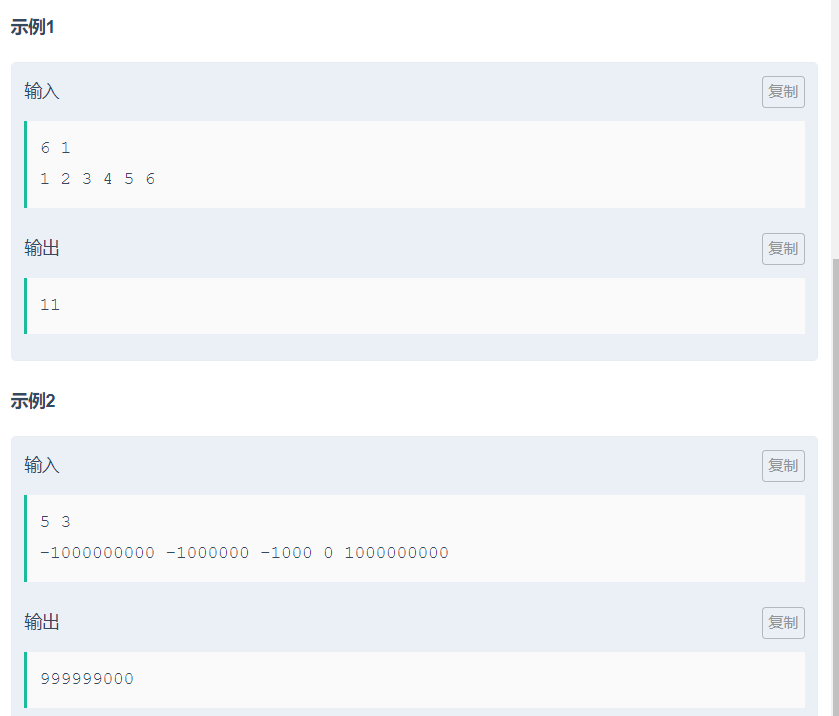
其实画一画很容易知道：偶数个的话，最多选\(\left \lfloor \frac{i}{2}\right \rfloor\)；奇数个的话，可以选\(\left \lfloor \frac{i}{2}\right \rfloor\)个也可以选\(\left \lfloor \frac{i}{2}\right \rfloor+1\)个

我们就设dp[i][0]表示前i个选了\(\left \lfloor \frac{i}{2}\right \rfloor\)个，dp[i][1]表示前i个选了\(\left \lfloor \frac{i}{2}\right \rfloor+1\)

AC_Code:

#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
#define endl '\n'
const int maxn = 2e5+10;
const ll inf=1e15;

ll a[maxn],dp[maxn][2];
int n,x;

int main()
{
    cin>>n>>x;
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    a[x]+=inf;

    dp[1][1]=a[1];
    for(int i=2;i<=n;i++){
        if( i%2==0 ){
            dp[i][0]=max(dp[i-1][1],dp[i-2][0]+a[i]);
        }else{
            dp[i][0]=max(dp[i-1][0],dp[i-2][0]+a[i]);
            dp[i][1]=dp[i-2][1]+a[i];
        }
    }
    cout<<dp[n][0]-inf<<endl;
    return 0;
}