一维差分基础

一维差分：（博客图片来源：here）

设有一个序列\(a_{1},a_{2},a_{3},\cdots ,a_{4}\)

我们定义一个新的序列：

\[\left\{\begin{matrix}
b_{i}=a_{i} & i=1\\
b_{i}=a_{i}-a_{i-1}& i\neq 1
\end{matrix}\right.\]

\(b\)数组就是\(a\)数组的差分数组

\(ps:\)差分的前缀和是原序列

差分应用一：

当我们要在某个区间\(\left [ l,r\right ]\)的所有值都加上一个数\(x\)时：我们只需要在差分数组中进行一加一减即可：\(b_{l}+x，b_{r+1}-x\)

 

 

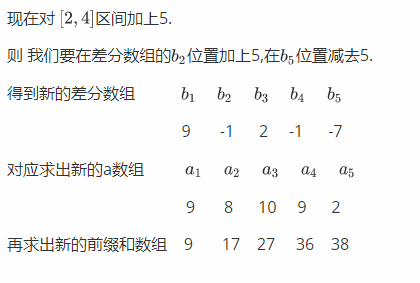
 查分应用二：快速求前缀和

\(设sum_{x}为以第x个数为结尾的前缀和，s_{i}为原数组，b_{i}为差分数组\)