基尔霍夫矩阵

Matrix-Tree 定理又称基尔霍夫矩阵树定理，其用于解决：给定 n 个点 m 条边的无向图，求图的生成树个数的问题。

【基尔霍夫矩阵】
1.基本定义
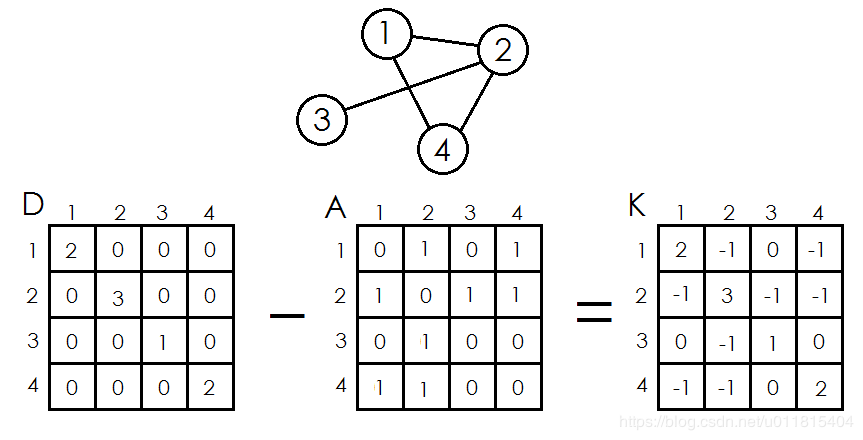
1）无向图 \(G\)：给定 \(n\) 个点，\(m\) 条边的无向图，设点集为 \(V\)，边集为 \(E\)，则其记为 \(G\left ( V,E\right )\)

2）度数矩阵 \(D\left [ G\right ]\)：当 \(i\neq j\) 时，\(D\left [ i\right ]\left [ j\right ]=0\)，当 \(i= j\) 时，\(D\left [ i\right ]\left [ j\right ]=点v的度数\)

3）邻接矩阵 \(A\left [ G\right ]\)：当 \(v_{i}\)、\(v_{j}\) 有边连接时，\(A\left [ i\right ]\left [ j\right ]=1\)，当 \(v_{i}\)、\(v_{j}\) 无边连接时，\(A\left [ i\right ]\left [ j\right ]=0\)

4）基尔霍夫矩阵(Kirchhoff) \(K\left [ G\right ]\)：也称拉普拉斯算子，其定义为 \(K\left [ G\right ]=D\left [ G\right ]-A\left [ G\right ]\)，即：\(K\left [ i\right ]\left [ j\right ]=D\left [ i\right ]\left [ j\right ]-A\left [ i\right ]\left [ j\right ]\)

例如：

 

 

2.基尔霍夫矩阵性质
对于任意一个图 \(G\)，其基尔霍夫矩阵 \(K\) 具有以下性质：

1.基尔霍夫矩阵 \(K\) 的每一行或每一列上的元素和都是 \(0\)
2.基尔霍夫矩阵 \(K\) 的行列式的值为 \(0\)
3.基尔霍夫矩阵 \(K\) 的任意一个代数余子式值都相同
4.如果图 \(G\) 不连通，基尔霍夫矩阵 \(K\) 的任意主子式行列式值为 \(0\)
5.如果图 \(G\) 是一棵树，基尔霍夫矩阵 \(K\) 的任意一个 \(n-1\) 阶主子式的行列式为 \(1\)

 

3.Matrix-Tree 定理
Matrix-Tree 定理的内容为：对于已经得出的基尔霍夫矩阵，去掉其随意一行一列得出的矩阵的行列式，其绝对值为生成树的个数

因此，对于给定的图 \(G\)，若要求其生成树个数，可以先求其基尔霍夫矩阵，然后随意取其任意一个 \(n-1\) 阶行列式，然后求出行列式的值，其绝对值就是这个图中生成树的个数。

 

基尔霍夫矩阵裸题：here

 

 

 

 模板：（AC_Code）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 20;
const int inf = 0x3f3f3f3f;
#define rep(i,first,second) for(ll i=first;i<=second;i++)
#define dep(i,first,second) for(ll i=first;i<=second;i++)
int degree[maxn];
ll a[maxn][maxn];
int vis[maxn][maxn];

void init(){
    memset(degree,0,sizeof(degree));
    memset(a,0,sizeof(a));
    memset(vis,0,sizeof(vis));
}

ll det(int n){
    ll ret=1;
    for(int i=2;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            while(a[j][i]){
                ll t=a[i][i]/a[j][i];
                for(int k=i;k<=n;k++){
                    a[i][k]=(a[i][k]-a[j][k]*t);
                }
                for(int k=i;k<=n;k++){
                    swap(a[i][k],a[j][k]);
                }
                
                ret=-ret;
            }
        }
        if( a[i][i]==0 ) return 0;
        ret*=a[i][i];
    }
    if( ret<0 ) ret=-ret;
    return ret;
}

int main()
{
    int t;
    scanf("%d",&t);
    while( t-- ){
        init();
        int n,m;
        scanf("%d%d",&n,&m);
        while( m--){
            int u,v;
            scanf("%d%d",&u,&v);
            a[u][u]++;
            a[v][v]++;
            a[u][v]--;
            a[v][u]--;
        }
        printf("%lld\n",det(n));
    }
    return 0;
}

参考博客：here