Dining(最大流建模经典例一)


题意:有N头牛,F种食物,D种饮料,每头牛都有喜欢的食物和饮料,每种饮料和食物只能分配给一头牛。最多有多少头牛能同时得到自己喜欢的食物和饮料。
思路:加源点和汇点。源点与食物,饮料和汇点的边容量都是1。一头牛拆分成两个点,两点之间的容量为1。喜欢的食物和饮料跟牛建条边,容量为1。这样完全就是最大流问题了。

图来源:here
AC_Code:
1 //#include <bits/stdc++.h> 2 #include <iostream> 3 #include <cstdio> 4 #include <algorithm> 5 #include <cmath> 6 #include <queue> 7 #include <string> 8 #include <cstring> 9 using namespace std; 10 typedef long long ll; 11 const int maxn = 1e5+10; 12 const int mod=1e9+7; 13 const int inf = 0x3f3f3f3f; 14 const double pi = acos(-0.1); 15 #define fi first 16 #define se second 17 #define pil pair<int,ll> 18 #define pli pair<ll,int> 19 #define pb push_back 20 #define rep(i,first,second) for(int i=first;i<=second;i++) 21 #define dep(i,first,second) for(int i=first;i>=second;i--) 22 23 struct node{ int to,w,nxt; }e[maxn<<1]; 24 int n,f,d; 25 int head[maxn<<1],dep[maxn],cnt; 26 27 void add(int u,int v,int w){ 28 e[cnt].to=v; 29 e[cnt].w=w; 30 e[cnt].nxt=head[u]; 31 head[u]=cnt++; 32 } 33 34 bool bfs(int st,int ed){ 35 memset(dep,-1,sizeof(dep)); 36 queue<int>que; 37 while( !que.empty()) que.pop(); 38 que.push(st); 39 dep[st]=0; 40 int u; 41 while(!que.empty()){ 42 u=que.front(); 43 que.pop(); 44 for(int i=head[u];~i;i=e[i].nxt){ 45 int v=e[i].to; 46 if( dep[v]==-1 && e[i].w>0 ){ 47 dep[v]=dep[u]+1; 48 que.push(v); 49 if( v==ed ) return true; 50 } 51 } 52 } 53 return dep[ed]!=-1; 54 } 55 56 int dfs(int st,int ed,int flow){ 57 if( st==ed || flow==0 ) return flow; 58 int curr=0; 59 for(int i=head[st];~i;i=e[i].nxt){ 60 int v=e[i].to,val=e[i].w; 61 if( dep[st]+1==dep[v] && val>0 ){ 62 int d=dfs(v,ed,min(val,flow)); 63 if( d>0 ){ 64 e[i].w-=d; 65 e[i^1].w+=d; 66 curr+=d; 67 flow-=d; 68 if( flow==0 ) break; 69 } 70 } 71 } 72 if( curr==0 ) dep[st]=inf; 73 return curr; 74 } 75 76 77 int Dinic(int st,int ed){ 78 int flow=0; 79 while( bfs(st,ed) ){ 80 flow+=dfs(st,ed,inf); 81 } 82 return flow; 83 } 84 //节点编号:源点:0 食物:1~f 饮料:(f+1)~(f+d) 牛:(f+d+1)~(f+d+2*n) 汇点:f+d+2*n+1 85 int main() 86 { 87 memset(head,-1,sizeof(head)); 88 scanf("%d%d%d",&n,&f,&d); 89 rep(i,1,f){//源点和食物之间建边 90 add(0,i,1); 91 add(i,0,0); 92 } 93 rep(i,1,n){ 94 int fi,di; 95 scanf("%d%d",&fi,&di); 96 rep(j,1,fi){//食物与左牛建边 97 int x; 98 scanf("%d",&x); 99 add(x,f+d+(2*i-1),1); 100 add(f+d+(2*i-1),x,0); 101 } 102 rep(j,1,di){//右牛与饮料建边 103 int x; 104 scanf("%d",&x); 105 add(f+d+2*i,f+x,1); 106 add(f+x,f+d+2*i,0); 107 } 108 } 109 for(int i=f+d+1;i<=f+d+2*n;i+=2){//左牛与右牛之间建边 110 add(i,i+1,1); 111 add(i+1,i,0); 112 } 113 rep(i,1,d){//饮料与汇点之间建边 114 add(f+i,f+d+2*n+1,1); 115 add(f+d+2*n+1,f+i,0); 116 } 117 118 int flag=Dinic(0,f+d+2*n+1); 119 printf("%d\n",flag); 120 return 0; 121 }
还有一道类似的题:
动物森友会(二分+网络流)

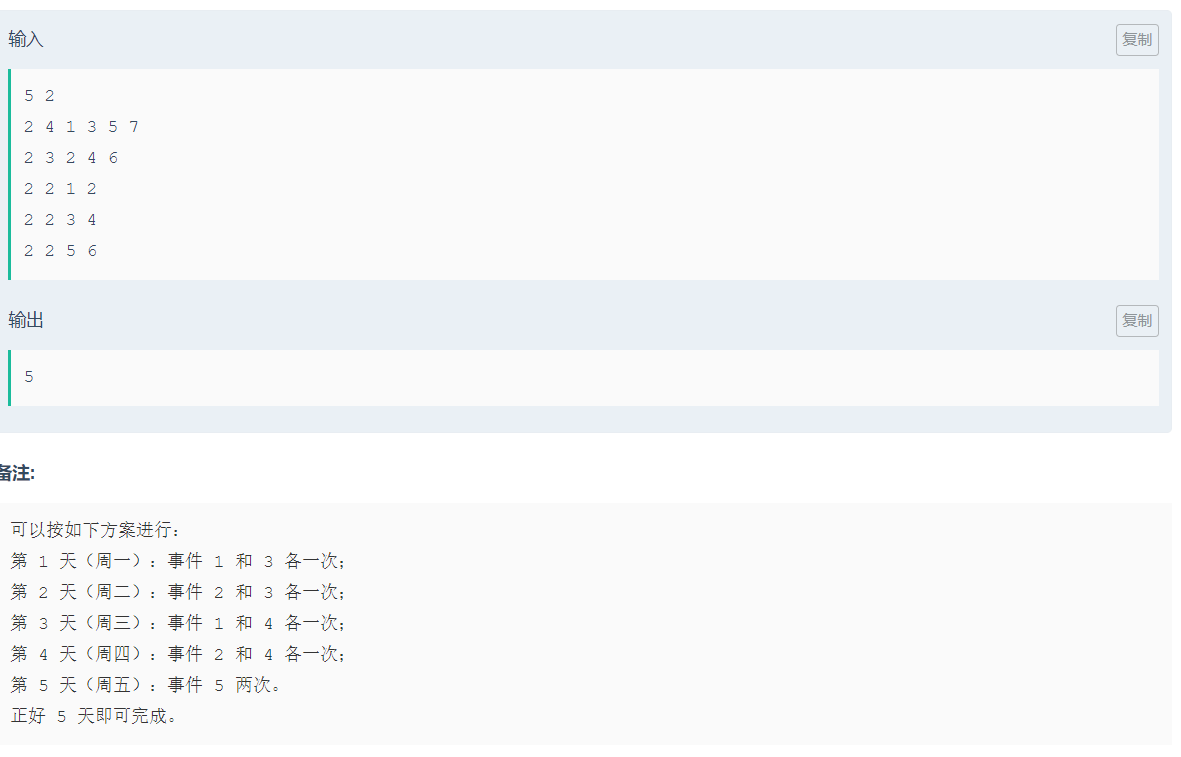
题解:二分答案找最少天数+网络流
1.建立源点,汇点
2.源点向week1-week7连边,第i天的流量上限是
\(\left ( \left \lfloor \frac{天数}{7}\right \rfloor+\left [ 天数mod7\geq i\right ]\right )\cdot 每天最多完成的事件数e\)
3.因为一个事件可以在同一天举行多次,我们也不知道具体多少次,所以week向事件连边时,设流量为inf
4.因为一个事件要完成的次数是限定的,所以我们设事件向汇点连边的容量为题目所给的ci
5.判断所给的天数内是否向汇点流入了题目要求的事件总数。

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define pb push_back 5 #define fi first 6 #define se second 7 #define pli pair<ll,int> 8 #define pil pair<int,ll> 9 typedef long long ll; 10 const int maxn = 1e4+10; 11 const int inf = 0x3f3f3f3f; 12 #define rep(i,first,second) for(int i=first;i<=second;i++) 13 #define dep(i,first,second) for(int i=first;i>=second;i--) 14 #define erep(u,i) for(int i=head[u];~i;i=e[i].nxt) 15 16 struct node{int to,nxt,c;}e[maxn<<1]; 17 int head[maxn<<1],ecnt,dep[maxn]; 18 void add(int u,int v,int val){ 19 e[ecnt]=(node){v,head[u],val}; 20 head[u]=ecnt++; 21 } 22 void Link(int u,int v,int w){ add(u,v,w),add(v,u,0);} 23 int dis[maxn],c[maxn]; 24 25 int n,E; 26 int sum,vc; 27 int a[maxn][10]; 28 int S,T; 29 30 bool bfs(){ 31 memset(dep,-1,sizeof(dep)); 32 queue<int>que; 33 while( !que.empty() ) que.pop(); 34 que.push(S);dep[S]=0; 35 while( !que.empty()){ 36 int u=que.front();que.pop(); 37 erep(u,i){ 38 int v=e[i].to,w=e[i].c; 39 if( dep[v]==-1 && w>0 ){ 40 dep[v]=dep[u]+1;que.push(v); 41 if( v==T) return true; 42 } 43 } 44 } 45 return dep[T]!=-1; 46 } 47 48 int dfs(int st,int flow){ 49 if( st==T || flow==0 ) return flow;; 50 int curr=0; 51 erep(st,i){ 52 int v=e[i].to,val=e[i].c; 53 if( dep[st]+1==dep[v] && val>0 ){ 54 int d=dfs(v,min(val,flow)); 55 if( d>0 ){ 56 e[i].c-=d;e[i^1].c+=d; 57 curr+=d;flow-=d; 58 if( flow==0 ) break; 59 } 60 } 61 } 62 if( curr==0 ) dep[st]=inf; 63 return curr; 64 } 65 66 int Dinic(){ 67 int ans=0; 68 while( bfs() ){ 69 ans+=dfs(S,inf); 70 } 71 return ans; 72 } 73 74 //源点:1 汇点:2 day:3~9 事件:9+1~9+n 75 int Check(int mid){ 76 if( E*mid<sum ) return 0; 77 memset(head,-1,sizeof(head));ecnt=vc=0; //init 78 S=++vc;T=++vc; //源点,汇点 79 80 rep(i,1,7){ //源点与day建边 81 Link(S,++vc,(mid/7+(mid%7>=i))*E); 82 } 83 rep(i,1,n){ 84 vc++; 85 Link(vc,T,c[i]); //事件与汇点建边 86 rep(j,1,7){ //事件与day建边 87 if( a[i][j] ){ 88 Link(j+2,vc,inf); 89 } 90 } 91 } 92 return Dinic()>=sum; 93 } 94 int main() 95 { 96 memset(head,-1,sizeof(head)); 97 scanf("%d%d",&n,&E); 98 rep(i,1,n){ 99 scanf("%d",&c[i]); 100 sum+=c[i]; 101 102 int mi; 103 scanf("%d",&mi); 104 rep(j,1,mi){ 105 int x; 106 scanf("%d",&x); 107 a[i][x]=1; 108 } 109 } 110 111 int l=0,r=1e9/E,res; 112 while( l<=r ){ 113 int mid=(l+r)>>1; 114 if( Check(mid) ){ 115 r=mid-1; 116 res=mid; 117 } 118 else l=mid+1; 119 } 120 printf("%d\n",res); 121 122 return 0; 123 }



