Drainage Ditches（最大流入门）

Drainage Ditches（最大流入门）

 

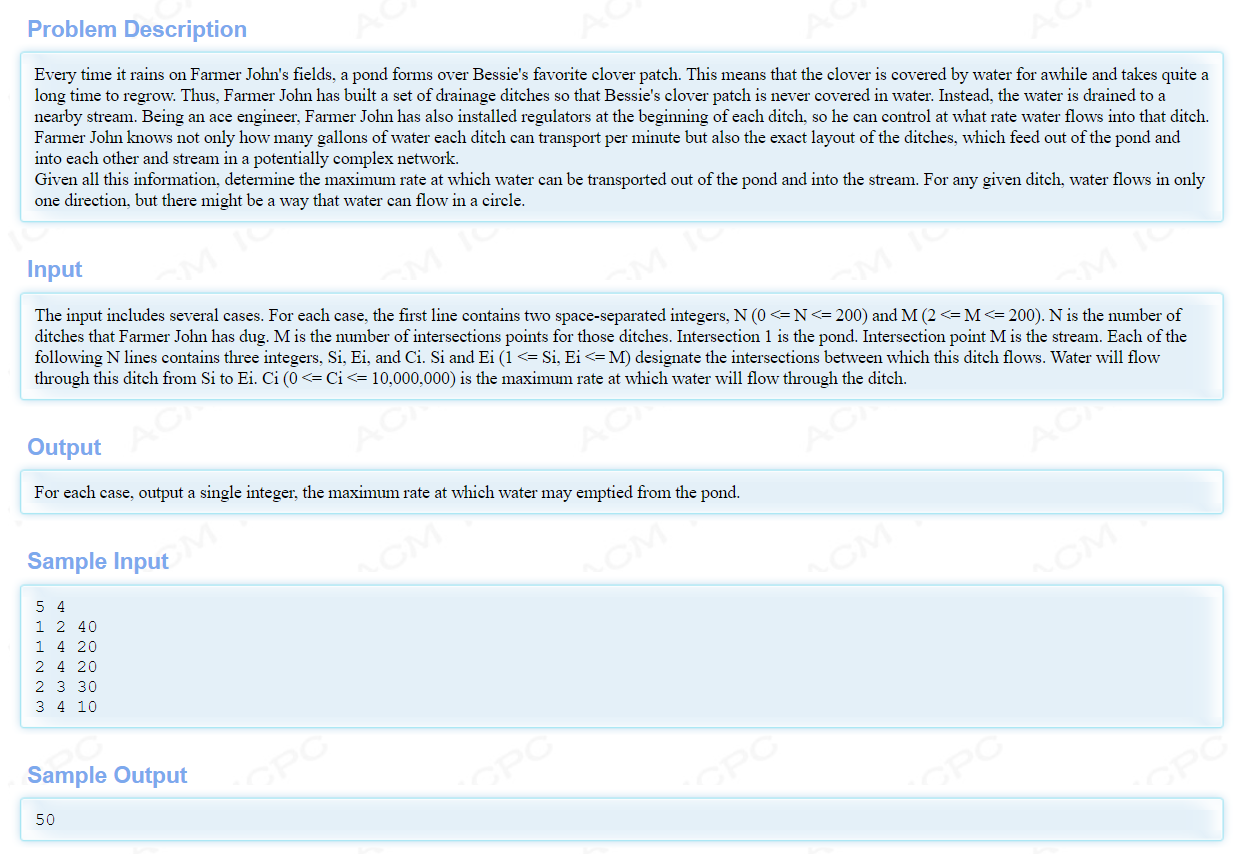
 EK+邻接矩阵：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
const int maxn=205;
const int inf=0x3f3f3f3f;
int graph[maxn][maxn];
int pre[maxn];//记录前驱节点
int vis[maxn];
int n,m,a,b,flow;

int BFS(int st,int ed){
    memset(vis,0,sizeof(vis));
    queue<int>que;
    while(!que.empty()) que.pop();
    que.push(st);
    vis[st]=1;
    int curr,flow=inf;
    pre[st]=pre[ed]=-1;
    while(!que.empty()){
        curr=que.front();
        que.pop();
        if( curr==ed ) break;
        rep(nxt,1,n){
            if(!vis[nxt]&&graph[curr][nxt]!=0){
                vis[nxt]=1;
                if( flow>graph[curr][nxt]) flow=graph[curr][nxt];
                pre[nxt]=curr;
                que.push(nxt);
            }
        }
    }
    if(pre[ed]==-1) return -1;//没有找到增广路
    return flow;
}

int EK(int st,int ed){
    int stream;
    int sum=0;
    while((stream=BFS(st,ed))!=-1 ){ //找到了增广路
        int u=ed;
        while( pre[u]!=-1 ){
            graph[pre[u]][u]-=stream;//改变正向边的容量
            graph[u][pre[u]]+=stream;//改变反向边的容量
            u=pre[u];
        }
        sum += stream;
    }
    return sum;
}
int main()
{
    while(~scanf("%d%d",&m,&n)){
        memset(graph,0,sizeof(graph));
        memset(vis,0,sizeof(vis));
        while( m-- ){
            scanf("%d%d%d",&a,&b,&flow);
            graph[a][b]+=flow;//此处注意可能出现多条同一起点终点的情况
        }
        printf("%d\n",EK(1,n));
    }
    return 0;
}

EK+前向星：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
int head[maxn<<1],cnt;
struct node{int to,nxt,val;}e[maxn<<1];
void addedge(int u,int v,int val){
    e[cnt].to=v;
    e[cnt].val=val;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}
int vis[maxn],pre[maxn];
int BFS(int st,int ed){
    memset(vis,0,sizeof(vis));
    vis[st]=1;
    queue<int>que;
    while(!que.empty()) que.pop();
    que.push(st);
    int u,v,flow=inf;
    pre[st]=pre[ed]=-1;
    while(!que.empty()){
        u=que.front();
        que.pop();
        if( u==ed ) break;
        for(int i=head[u];~i;i=e[i].nxt ){
            v=e[i].to;
            if(!vis[v]&&e[i].val>0){
                vis[v]=1;
                flow=min(flow,e[i].val);
                pre[v]=i;//注意是i,不是u
                que.push(v);
            }
        }
    }
    if( pre[ed]==-1 ) return -1;
    return flow;
}
int EK(int st,int ed){
    int stream,flow=0;
    while((stream=BFS(st,ed))!=-1 ){
        //pre通过节点存边的坐标,通过边的反向边的to获取上一个节点
        for(int i=pre[ed];~i;i=pre[e[i^1].to]){
            e[i].val-=stream;
            e[i^1].val+=stream;
        }
        flow+=stream;
    }
    return flow;
}
int main()
{
    int a,b,n,m,flow;
    while(~scanf("%d%d",&m,&n)){
        memset(head,-1,sizeof(head));
        cnt=0;
        while( m-- ){
            scanf("%d%d%d",&a,&b,&flow);
            addedge(a,b,flow);
            addedge(b,a,0);
        }
        printf("%d\n",EK(1,n));
    }
    return 0;
}

 

FF+邻接矩阵：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
int graph[maxn][maxn];
int vis[maxn];
int n,m;
int dfs(int st,int ed,int f){//在没有走到汇点前我们不知道流量是多少,所以f是动态更新的
    vis[st]=1;
    if(st==ed) return f;//走到汇点返回本次增广的流量
    rep(i,1,n){
        if( graph[st][i]>0 && vis[i]==0 ){
            int d=dfs(i,ed,min(graph[st][i],f));
            if( d>0 ){//顺着流过去,要受一路上最小容量的限制
                graph[st][i]-=d;
                graph[i][st]+=d;
                return d;
            }
        }
    }
    return 0;//无法到汇点
}
int FF(int st,int ed){
    int flow=0,curr;
    while(1){
        memset(vis,0,sizeof(vis));
        curr=dfs(st,ed,inf);
        if( curr==0 ) return flow;
        flow+=curr;
    }
}
int main()
{
    int a,b,val;
    while(~scanf("%d%d",&m,&n)){
        memset(graph,0,sizeof(graph));
        while(m--){
            scanf("%d%d%d",&a,&b,&val);
            graph[a][b]+=val;
        }
        printf("%d\n",FF(1,n));
    }
    return 0;
}

 

FF+邻接表：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
struct node{
    int to;
    int flow;
    int rev;//反向边在数组中的位置
    node(){}
    node(int to,int flow,int rev):to(to),flow(flow),rev(rev){}
};
vector<node>graph[maxn];
int vis[maxn];
int n,m;
void addedge(int from,int to,int val){
    graph[from].push_back(node(to,val,graph[to].size()));
    graph[to].push_back(node(from,0,graph[from].size()-1));
}
int dfs(int st,int ed,int f){
    vis[st]=1;
    if(st==ed)return f;
    rep(i,0,graph[st].size()-1){
        node &temp=graph[st][i];//注意必须用引用
        if(!vis[temp.to] && temp.flow>0 ){
            int d=dfs(temp.to,ed,min(f,temp.flow));
            if( d>0 ){
                temp.flow-=d;
                graph[temp.to][temp.rev].flow+=d;
                return d;
            }
        }
    }
    return 0;
}
int FF(int st,int ed){
    int flow=0,curr;
    while(1){
        memset(vis,0,sizeof(vis));
        curr=dfs(st,ed,inf);
        if( curr==0 ) return flow;
        flow+=curr;
    }
}
int main()
{
    int a,b,val;
    while(~scanf("%d%d",&m,&n)){
        rep(i,1,n) graph[i].clear();
        while( m-- ){
            scanf("%d%d%d",&a,&b,&val);
            addedge(a,b,val);
        }
        printf("%d\n",FF(1,n));
    }
    return 0;
}

 

FF+前向星： 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
struct node{int to,nxt,c;}e[maxn<<1];
int head[maxn<<1],cnt,vis[maxn];
void addedge(int u,int v,int val){
    e[cnt].to=v;
    e[cnt].c=val;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}
int dfs(int st,int ed,int f){
    vis[st]=1;
    if(st==ed) return f;
    for(int i=head[st];~i;i=e[i].nxt){
        int v=e[i].to,val=e[i].c;
        if( !vis[v]&&val>0 ){
            int d=dfs(v,ed,min(val,f));
            if( d>0 ){
                e[i].c-=d;
                e[i^1].c+=d;
                return d;
            }
        }
    }
    return 0;
}
int FF(int st,int ed){
    int flow=0,d;
    while(1){
        memset(vis,0,sizeof(vis));
        d=dfs(st,ed,inf);
        if(d==0) return flow;
        flow+=d;
    }
}
int main()
{
    int n,m,a,b,val;
    while(~scanf("%d%d",&m,&n)){
        memset(head,-1,sizeof(head));
        cnt=0;
        while( m-- ){
            scanf("%d%d%d",&a,&b,&val);
            addedge(a,b,val);
            addedge(b,a,0);
        }
        printf("%d\n",FF(1,n));
    }
    return 0;
}

 

Dinic+邻接矩阵：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
int graph[maxn][maxn];
int step[maxn];//相当于将图分层了
int n,m;
bool bfs(int st,int ed){//bool 函数是一个小优化，判断是否能搜到汇点,如果连汇点都搜不到还dfs干什么
    memset(step,-1,sizeof(step));
    queue<int>que;
    while(!que.empty()) que.pop();
    step[st]=0;
    que.push(st);
    while(!que.empty()){
        int curr=que.front();
        que.pop();
        rep(i,1,n){
            if(graph[curr][i]>0 && step[i]==-1 ){
                step[i]=step[curr]+1;
                if( i==ed ) return true;
                que.push(i);
            }
        }
    }
    return step[ed]!=-1;
}
int dfs(int st,int ed,int f){
    if(st==ed||f==0) return f;
    int flow=0,d;
    rep(i,1,n){
        if((step[i]==step[st]+1)&&graph[st][i]>0&&(d=dfs(i,ed,min(graph[st][i],f)))){//step[i]==step[st]+1;控制仅允许流向下一层
            graph[st][i]-=d;
            graph[i][st]+=d;
            flow+=d;//累加当前节点的某条路径的合适流量
            f-=d;//当前节点的容量减去某条路径的合适流量
            if(f==0) break;//如果当前节点的容量用完,说明无法再通过任何流量
        }
    }
    if( flow==0 ) step[st]=inf;//如果当前节点无任何流量通过,取消标记
    return flow;
}
int Dinic(int st,int ed){
    int flow=0;
    while(bfs(st,ed)){
        flow+=dfs(st,ed,inf);
    }
    return flow;
}
int main()
{
    int a,b,flow;
    while(~scanf("%d%d",&m,&n)){
        memset(graph,0,sizeof(graph));
        while(m--){
            scanf("%d%d%d",&a,&b,&flow);
            graph[a][b]+=flow;
        }
        printf("%d\n",Dinic(1,n));
    }
    return 0;
}

 

Dinic+邻接表：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
int step[maxn];
struct node{
    int to;
    int flow;
    int rev;//记录反向边的index
    node(){}
    node(int to,int flow,int rev):to(to),flow(flow),rev(rev){}
};
vector<node>graph[maxn];
int n,m;
void addedge(int from,int to,int flow){
    graph[from].push_back(node(to,flow,graph[to].size()));
    graph[to].push_back(node(from,0,graph[from].size()-1));
}
bool bfs(int st,int ed){
    memset(step,-1,sizeof(step));
    queue<int>que;
    que.push(st);
    step[st]=0;
    while(!que.empty()){
        int curr=que.front();
        que.pop();
        rep(i,0,graph[curr].size()-1){
            node &temp=graph[curr][i];
            if(step[temp.to]==-1 && temp.flow>0 ){
                step[temp.to]=step[curr]+1;
                if( temp.to==ed ) return true;
                que.push(temp.to);
            }
        }
    }
    return step[ed]!=-1;
}
int dfs(int st,int ed,int f){
    if( st==ed || f==0 ) return f;
    int flow=0;
    rep(i,0,graph[st].size()-1){
        node &temp=graph[st][i];
        if( temp.flow>0 && step[temp.to]==step[st]+1){
            int d=dfs(temp.to,ed,min(f,temp.flow));
            if(d>0){
                temp.flow-=d;
                graph[temp.to][temp.rev].flow+=d;
                flow+=d;
                f-=d;
                if(f==0) break;
            }
        }
    }
    if( flow==0 ) step[st]=inf;
    return flow;
}
int Dinic(int st,int ed){
    int flow=0;
    while(bfs(st,ed)){
        flow+=dfs(st,ed,inf);
    }
    return flow;
}
int main()
{
    int a,b,flow;
    while(~scanf("%d%d",&m,&n)){
        memset(graph,0,sizeof(graph));
        while( m-- ){
            scanf("%d%d%d",&a,&b,&flow);
            addedge(a,b,flow);
        }
        printf("%d\n",Dinic(1,n));
    }
    return 0;
}

 

Dinic+前向星：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
int head[maxn<<1],cnt,step[maxn];
struct node{int to,nxt,c;}e[maxn<<1];
void addedge(int u,int v,int val){
    e[cnt].to=v;
    e[cnt].c=val;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}
bool bfs(int st,int ed){
    memset(step,-1,sizeof(step));
    queue<int>que;
    while(!que.empty())que.pop();
    que.push(st);
    step[st]=0;
    int u;
    while(!que.empty()){
        u=que.front();
        que.pop();
        for(int i=head[u];~i;i=e[i].nxt){
            int v=e[i].to;
            if( step[v]==-1 && e[i].c>0 ){
                step[v]=step[u]+1;
                que.push(v);
                if( v==ed ) return true;
            }
        }
    }
    return step[ed]!=-1;
}

int dfs(int st,int ed,int flow){
    if(st==ed||flow==0) return flow;
    int curr=0;
    for(int i=head[st];~i;i=e[i].nxt){
        int v=e[i].to;
        int val=e[i].c;
        if( step[st]+1==step[v] && val>0 ){
            int d=dfs(v,ed,min(val,flow));
            if(d>0){
                e[i].c-=d;
                e[i^1].c+=d;//添反向边的时候是相邻的,i^1取相邻数;
                curr+=d;//累加当前节点的某条路径的合适流量
                flow-=d;//当前节点的容量减去某条路径的合适流量
                if(flow==0) break;//如果当前节点的容量用完,说明无法再通过任何流量
            }
        }
    }
    if( curr==0 ) step[st]=inf;//如果当前节点无任何流量通过,取消标记
    return curr;
}

int Dinic(int st,int ed){
    int flow=0;
    while(bfs(st,ed)){
        flow+=dfs(st,ed,inf);
    }
    return flow;
}
int main()
{
    int n,m,a,b,val;
    while(~scanf("%d%d",&m,&n)){
        memset(head,-1,sizeof(head));
        cnt=0;
        while(m--){
            scanf("%d%d%d",&a,&b,&val);
            addedge(a,b,val);
            addedge(b,a,0);
        }
        printf("%d\n",Dinic(1,n));
    }
    return 0;
}

 

Dinic+前向星+优化：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=210;
const int inf=0x3f3f3f3f;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
int head[maxn<<1],cnt,step[maxn],cur[maxn];
struct node{int to,nxt,c;}e[maxn<<1];
void addedge(int u,int v,int val){
    e[cnt].to=v;
    e[cnt].c=val;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}
bool bfs(int st,int ed){
    memset(step,-1,sizeof(step));
    queue<int>que;
    while(!que.empty())que.pop();
    que.push(st);
    step[st]=0;
    int u;
    while(!que.empty()){
        u=que.front();
        que.pop();
        for(int i=head[u];~i;i=e[i].nxt){
            int v=e[i].to;
            if( step[v]==-1 && e[i].c>0 ){
                step[v]=step[u]+1;
                que.push(v);
                if( v==ed ) return true;
            }
        }
    }
    return step[ed]!=-1;
}

int dfs(int st,int ed,int flow){
    if(st==ed||flow==0) return flow;
    int curr=0;
    for(int &i=cur[st];~i;i=e[i].nxt){
        int v=e[i].to;
        int val=e[i].c;
        if( step[st]+1==step[v] && val>0 ){
            int d=dfs(v,ed,min(val,flow));
            if(d>0){
                e[i].c-=d;
                e[i^1].c+=d;
                curr+=d;
                flow-=d;
                if(flow==0) break;
            }
        }
    }
    if( curr==0 ) step[st]=inf;
    return curr;
}

int Dinic(int st,int ed){
    int flow=0;
    while(bfs(st,ed)){
        rep(i,0,maxn-2) cur[i]=head[i];
        flow+=dfs(st,ed,inf);
    }
    return flow;
}
int main()
{
    int n,m,a,b,val;
    while(~scanf("%d%d",&m,&n)){
        memset(head,-1,sizeof(head));
        cnt=0;
        while(m--){
            scanf("%d%d%d",&a,&b,&val);
            addedge(a,b,val);
            addedge(b,a,0);
        }
        printf("%d\n",Dinic(1,n));
    }
    return 0;
}