H. Reporting on Mars

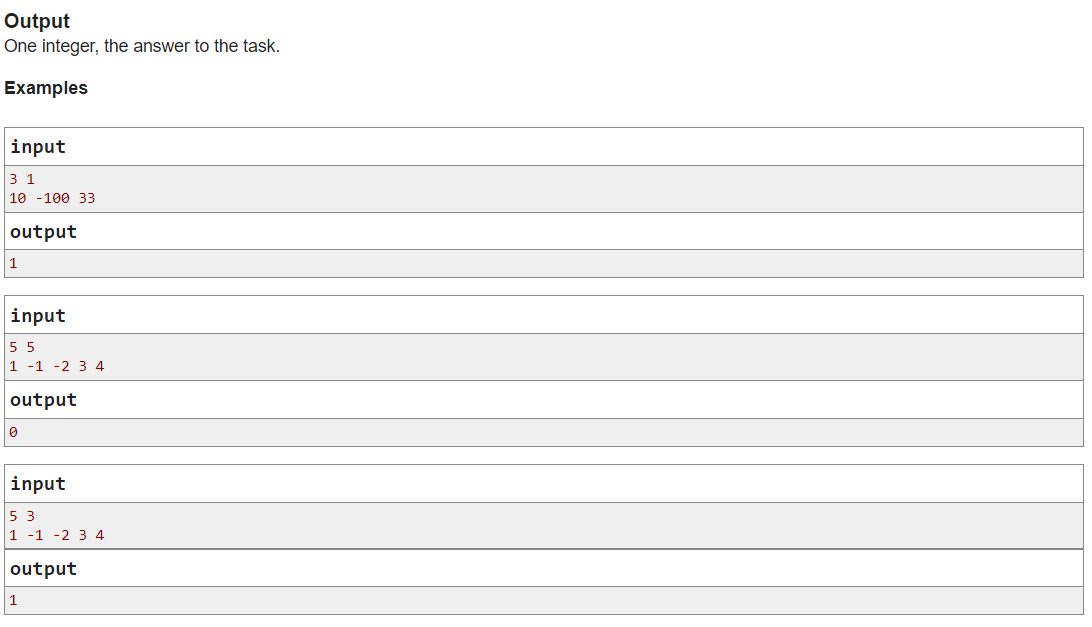
题意:给定n个数的数组,以及一个数k,每次操作可以把一个正数换成一个负数,把一个负数换成一个整数,问最少操作几次可以满足每个\(a[i]\rightarrow a[i+(k-1)]\)之间的数乘起来之后大于0
分析:序号相差k(下文我称他们为“同相位”)的数字,满足题目条件时正负性一定相等。
num[i%k][0];表示同“相位”的数是负数的个数
num[i%k][1];表示同“相位”的数是正数的个数
\(dp[i][0]\);表示每一组前i+1个数相乘的结果为负数的转变正负次数的最优解(即转变正负次数最小值)
\(dp[i][1]\);表示每一组前i+1个数相乘的结果为正数的转变正负次数的最优解(即转变正负次数最小值)
初始化:\(dp[0][0]=num[0][1]\),前1个数为负,则前1个数要转变的次数为原来是正数的个数
\(dp[0][1]=num[0][0]\);前1个数为正,则前1个数要转变的次数为原来是负数的个数
AC_Code:
1 #include <iostream> 2 #include <bits/stdc++.h> 3 using namespace std; 4 typedef long long ll; 5 const int maxn = 5e5+10; 6 const int inf=0x3f3f3f3f; 7 #define rep(i,first,last) for(int i=first;i<=last;i++) 8 #define dep(i,first,last) for(int i=first;i>=last;i--) 9 int n,k; 10 int dp[maxn][2],num[maxn][2]; 11 int main() 12 { 13 scanf("%d%d",&n,&k); 14 rep(i,0,n-1){ 15 int x; 16 scanf("%d",&x); 17 num[i%k][x>0]++; 18 } 19 dp[0][0]=num[0][1]; 20 dp[0][1]=num[0][0]; 21 rep(i,1,k-1){ 22 dp[i][0]=min(dp[i-1][0]+num[i][0],dp[i-1][1]+num[i][1]); 23 dp[i][1]=min(dp[i-1][0]+num[i][1],dp[i-1][1]+num[i][0]); 24 } 25 printf("%d\n",dp[k-1][1]); 26 return 0; 27 }


