蓝魔法师

蓝魔法师

 

 

 

 

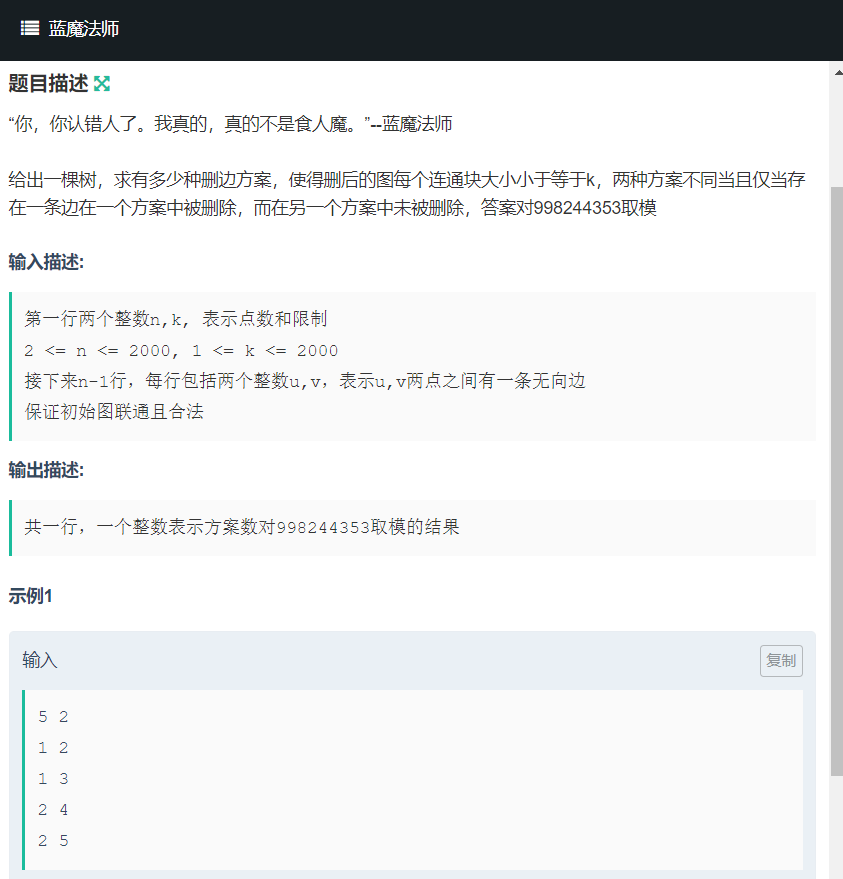
 分析：sz保存包括自身的所有子孙总节点数(为了求连通块的大小做准备)

dp[i][j]表示只考虑根为i的子树,包含节点i的联通块大小为j的方案个数

dp[i][0]表示dp[i][1]+...+dp[i][k]

一棵子树根节点为u的连通块（包括u）对于它的一个子节点v，当u访问到v时，假设之前已经访问了几个子节点，

之前访问的节点个数为sz[u]，那么假设我们要让连通块大小为p，p可以从两个地方来：

从之前访问过的节点中，也就是sz【u】，也可以从现在正在访问的节点v，也就是sz【v】

u提供连通分量的j个 v(u的子节点，与u相连)提供k个，连起来该连通分量大小就是k+j

乘法原理方案总个数为dp[u][j]*dp[v][k];

总结：dp_i,u+v=∑(dp_i,u∗dp_son,v)

　　　dp_i,0=∑f_i,j(j<=k)

　　　dp_i,j=0,j>K

AC_Code

 

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e3+10;
const int inf=0x3f3f3f3f;
const int mod=998244353;
#define rep(i,first,last) for(int i=first;i<=last;i++)
#define dep(i,first,last) for(int i=first;i>=last;i--)
struct edge{ll to,nxt;}e[maxn<<1];
ll dp[maxn][maxn],sz[maxn],tmp[maxn];
ll n,m,u,v,cnt,head[maxn<<1];
void addedge(ll u,ll v){
    e[cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}
void add(ll &x,ll y){ x=(x+y>=mod?x+y-mod:x+y);}
void dfs(ll u,ll fa){
    sz[u]=1;
    dp[u][1]=1;
    for(ll i=head[u];~i;i=e[i].nxt){
        ll v=e[i].to;
        if( v!=fa ){
            dfs(v,u);
            rep(j,1,sz[u]+sz[v]) tmp[j]=0;//初始化
            rep(j,0,sz[u]){
                rep(k,0,sz[v]){
                    add(tmp[j+k],1ll*dp[v][k]*dp[u][j]%mod);
                }
            }
            sz[u]+=sz[v];
            rep(j,1,sz[u]) dp[u][j]=tmp[j];
        }
    }
    dp[u][0]=0;
    rep(j,1,m) add(dp[u][0],dp[u][j]);
    rep(j,m+1,sz[u]) dp[u][j]=0;
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%lld%lld",&n,&m);
    rep(i,1,n-1){
        ll u,v;
        scanf("%lld%lld",&u,&v);
        addedge(u,v);
        addedge(v,u);
    }
    dfs(1,0);
    printf("%lld\n",dp[1][0]);
    return 0;
}