H. Pavel's Party(权值线段树)

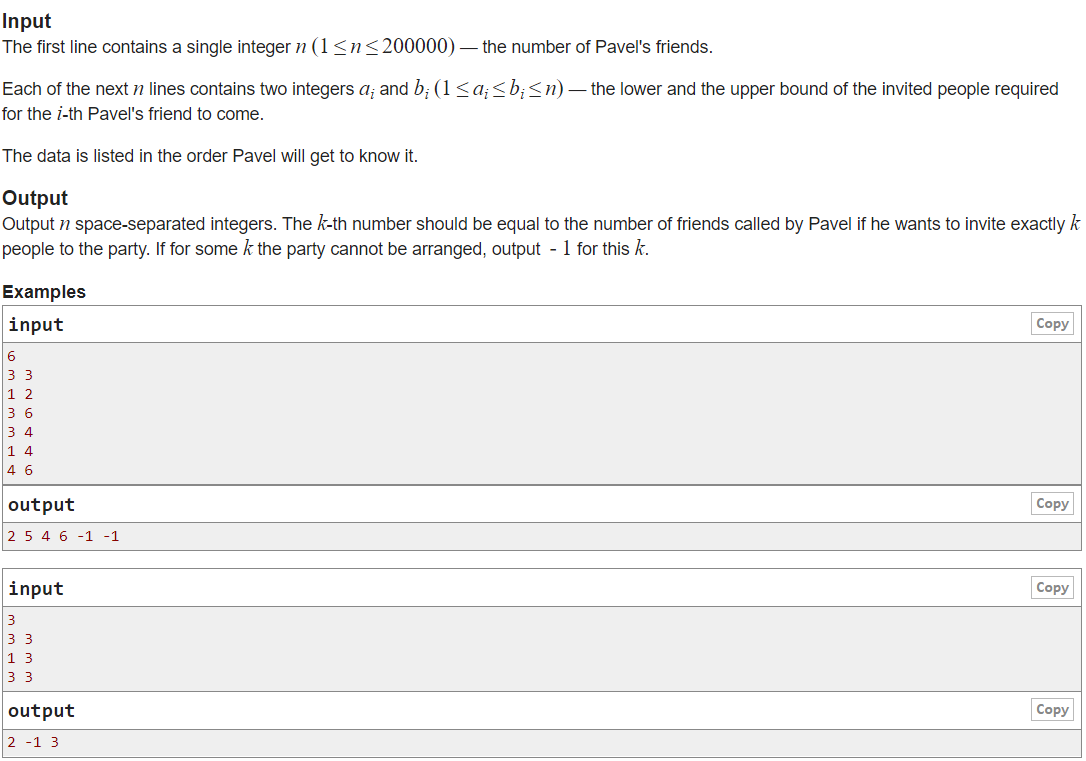
题意:Pavel 将要举行一个聚会,他想确切地邀请k个人参加。他有n个朋友,并且他已经决定按什么顺序打电话和邀请他们,每个朋友会回复他两个值 l 和 r,代表如果Pavel准备邀请的人数在[ l, r ] 之间他就会参加。Pavel一旦集合了所需的人数,就会立刻开启聚会,不会给其余的朋友打电话。询问k为1~n时,分别,最少需要给前多少人打电话。如果给n个朋友全打完也凑不到人就输出-1.
样例一解释:6个朋友,分别给出ai bi,
输出的2表示当Pavel准备组织1个人的聚会需要给前2个人打电话。(1不来,2来)
输出的5表示当Pavel准备组织2个人的聚会需要给前5个人打电话。(2来,5来)
输出的4表示当Pavel准备组织3个人的聚会需要给前4个人打电话。(1,3,4来)
输出的6表示当Pavel准备组织4个人的聚会需要给前6个人打电话。(3,4,5,6来)
最后要邀请5个人,或者6个人,即使6个朋友的电话都打完,也没有凑够人
思路:我们做一颗权值线段树维护所有编号对应的人的信息(来或不来)。当为1时,表示这个人可以来; 为0时,表示这个人不来。准备两个数组(里面存每个人的 l ,r,id),一个是左边界升序(a数组)(一个人来(进入线段树)的边界),一个是右边界升序(b数组)(一个人不来(离开线段树)的边界)。
AC_Code
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define rep(i,first,last) for(int i=first;i<=last;i++) 4 #define dep(i,first,last) for(int i=first;i>=last;i--) 5 #define lowbit(x) (x&(-x)) 6 7 typedef long long ll; 8 const int maxn = 2e5+10; 9 struct node{ 10 int ai; 11 int bi; 12 int id; 13 }a[maxn],b[maxn]; 14 int n,ans[maxn]; 15 int tree[maxn<<2]; 16 bool cmp1(node x, node y){return x.ai<y.ai;} 17 bool cmp2(node x, node y){return x.bi<y.bi;} 18 void updata(int rt,int l, int r, int k, int val){ 19 if( l==r ){ 20 tree[rt]+=val; 21 return ; 22 } 23 int mid=(l+r)>>1; 24 if( k>mid ) updata(rt<<1|1,mid+1,r,k,val); 25 else updata(rt<<1,l,mid,k,val); 26 tree[rt]=tree[rt<<1]+tree[rt<<1|1]; 27 } 28 29 int query(int rt,int l,int r,int k){ 30 int mid=(l+r)>>1; 31 if( l==r ) return l; 32 else if( tree[rt<<1]<k ) return query(rt<<1|1,mid+1,r,k-tree[rt<<1]); 33 else if( tree[rt<<1]>=k ) return query(rt<<1,l,mid,k); 34 } 35 36 int main(){ 37 scanf("%d",&n); 38 rep(i,1,n){ 39 scanf("%d%d",&a[i].ai,&a[i].bi); 40 a[i].id=i; 41 b[i].ai=a[i].ai; b[i].bi=a[i].bi; b[i].id=i; 42 } 43 sort(a+1,a+1+n,cmp1); 44 sort(b+1,b+1+n,cmp2); 45 int pos1=1,pos2=1; 46 rep(k,1,n){ 47 while( pos1<=n && a[pos1].ai==k ){ 48 updata(1,1,n,a[pos1].id,1); 49 pos1++; 50 } 51 if( tree[1]<k ) ans[k]=-1; 52 else ans[k]=query(1,1,n,k); 53 while( pos2<=n && b[pos2].bi==k ){ 54 updata(1,1,n,b[pos2].id,-1); 55 pos2++; 56 } 57 } 58 rep(i,1,n){ 59 if( i==1 ) printf("%d",ans[i]); 60 else printf(" %d",ans[i]); 61 } 62 printf("\n"); 63 return 0; 64 }

