权值线段树入门
AC_Code
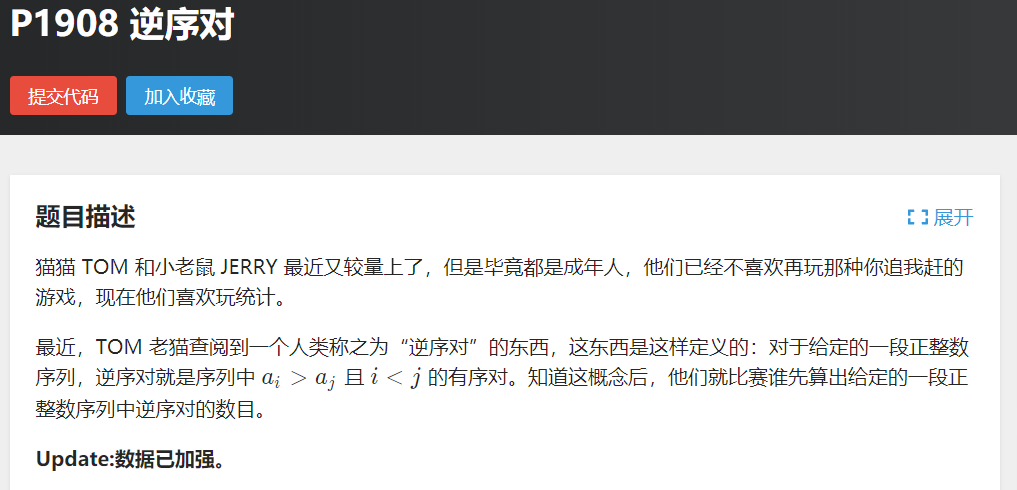
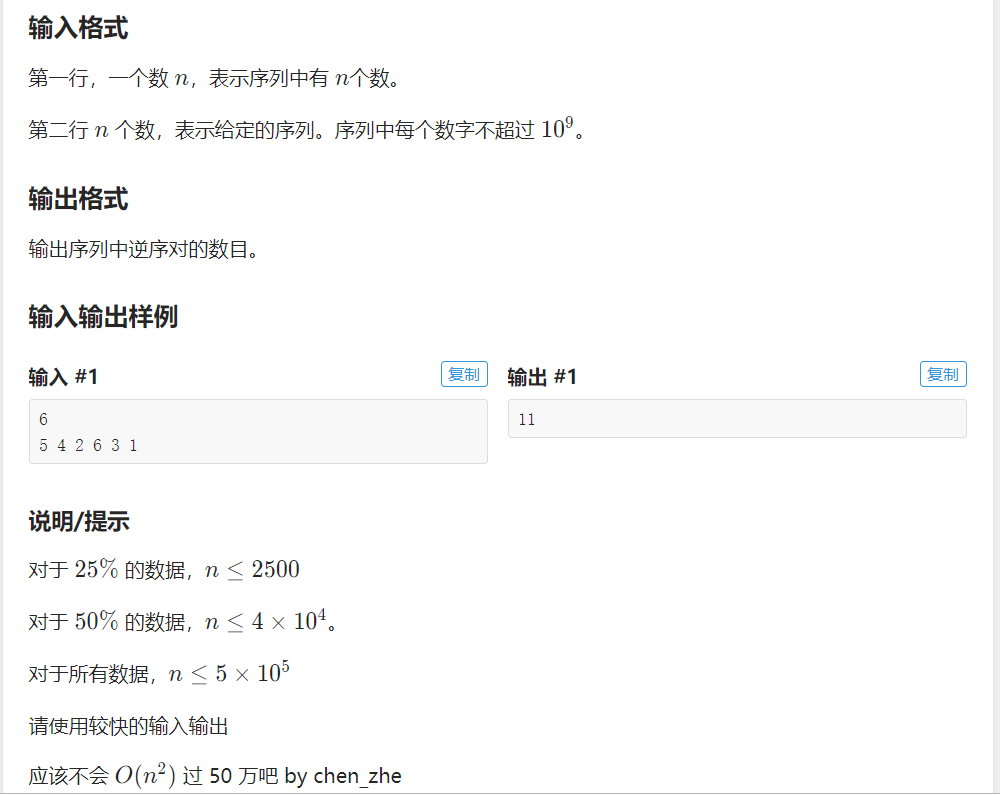
1 //权值线段树: 2 //区间的值是这段值域里的个数的线段树 3 //叶子结点的值 是这个数在序列里出现的次数 4 //能够比较容易实现平衡树的一系列操作 5 //权值线段树就是把线段树的每个点权权值线段树就是把线段树的每个点权,赋予一定的含义,比如数字出现的次数,数值前缀出现的次数,并用区间求和维护一个前缀信息,比如数字出现的次数,第K大等(不能实现区间第K大),前缀第K大等 6 #include <bits/stdc++.h> 7 using namespace std; 8 typedef long long ll; 9 const int maxn = 5e5+10; 10 const int inf=0x3f3f3f3f; 11 #define lowbit(x) ((x)&(-x)) 12 #define rep(i,first,last) for(int i=first;i<=last;i++) 13 #define dep(i,first,last) for(int i=first;i>=last;i--) 14 15 ll a[maxn]; 16 int tree[maxn<<2]; 17 vector<ll>vec; 18 int n; 19 void getid(){ 20 sort(vec.begin(),vec.end()); 21 vec.erase(unique(vec.begin(),vec.end()),vec.end()); 22 rep(i,1,n){ 23 a[i]=lower_bound(vec.begin(),vec.end(),a[i])-vec.begin()+1; 24 } 25 return ; 26 } 27 28 void updata(int rt,int x,int l,int r){ 29 tree[rt]++; 30 if( l==r ) return ; 31 int mid=(l+r)>>1; 32 if( x>mid ) updata(rt<<1|1,x,mid+1,r); 33 else updata(rt<<1,x,l,mid); 34 } 35 36 ll query(int rt,int L,int R, int l,int r){ 37 if( L<=l && R>=r ) return tree[rt]; 38 int mid=(l+r)>>1; 39 if( L>mid ) return query(rt<<1|1,L,R,mid+1,r); 40 else if( R<=mid ) return query(rt<<1,L,R,l,mid); 41 else return query(rt<<1,L,R,l,mid)+query(rt<<1|1,L,R,mid+1,r); 42 } 43 44 int main() 45 { 46 vec.clear(); 47 scanf("%d",&n); 48 rep(i,1,n){ 49 scanf("%lld",&a[i]); 50 vec.push_back(a[i]); 51 } 52 getid(); 53 int len=vec.size(); 54 ll ans=0; 55 rep(i,1,n){ 56 updata(1,a[i],1,len); 57 if( a[i]==len ) continue; 58 ans += query(1,a[i]+1,len,1,len); 59 } 60 printf("%lld\n",ans); 61 return 0; 62 }


AC_Code
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1e5+3; 5 const int inf=0x3f3f3f3f; 6 #define lowbit(x) ((x)&(-x)) 7 #define rep(i,first,last) for(int i=first;i<=last;i++) 8 #define dep(i,first,last) for(int i=first;i>=last;i--) 9 int tree[maxn<<2],a[maxn],op[maxn]; 10 int n; 11 vector<int>v; 12 13 int getid(int t){ 14 return lower_bound(v.begin(),v.end(),t)-v.begin()+1; 15 } 16 17 void updata(int rt, int x, int l, int r, int k){ 18 if(l==r){ 19 tree[rt]+=k; 20 return ; 21 } 22 int mid=(l+r)>>1; 23 if( x>mid ) updata(rt<<1|1,x,mid+1,r,k); 24 else updata(rt<<1,x,l,mid,k); 25 tree[rt]=tree[rt<<1]+tree[rt<<1|1]; 26 } 27 28 int query_small(int L,int R,int l,int r,int rt){ 29 if(L>R) return 0; 30 if( L<=l && R>=r ) return tree[rt]; 31 int mid=(l+r)>>1; 32 if( L>mid ) return query_small(L,R,mid+1,r,rt<<1|1); 33 else if( R<=mid ) return query_small(L,R,l,mid,rt<<1); 34 else return query_small(L,R,l,mid,rt<<1)+query_small(L,R,mid+1,r,rt<<1|1); 35 } 36 37 int Kth(int rt,int k,int l,int r){ 38 if( l==r ) return l; 39 int mid=(l+r)>>1; 40 if( tree[rt<<1]>=k ) return Kth(rt<<1,k,l,mid); 41 else return Kth(rt<<1|1,k-tree[rt<<1],mid+1,r); 42 } 43 44 int main() 45 { 46 scanf("%d",&n); 47 rep(i,1,n){ 48 scanf("%d%d",&op[i],&a[i]); 49 if( op[i]!=4 ) v.push_back(a[i]); 50 } 51 sort(v.begin(),v.end()); 52 v.erase(unique(v.begin(),v.end()),v.end()); 53 int len=v.size(); 54 rep(i,1,n){ 55 if( op[i]==1 ) updata(1,getid(a[i]),1,len,1); 56 else if( op[i]==2 ) updata(1,getid(a[i]),1,len,-1); 57 else if( op[i]==3 ){ 58 if( a[i]==1 ) printf("1\n"); 59 else printf("%d\n",query_small(1,getid(a[i])-1,1,len,1)+1); 60 } 61 else if( op[i]==4 ) printf("%d\n",v[Kth(1,a[i],1,len)-1]); 62 else if( op[i]==5 ) { 63 int pre=query_small(1,getid(a[i])-1,1,len,1); 64 printf("%d\n",v[Kth(1,pre,1,len)-1]); 65 } 66 else if( op[i]==6 ){ 67 int bac=query_small(1,getid(a[i]),1,len,1); 68 printf("%d\n",v[Kth(1,bac+1,1,len)-1]); 69 } 70 } 71 return 0; 72 }

AC_Code
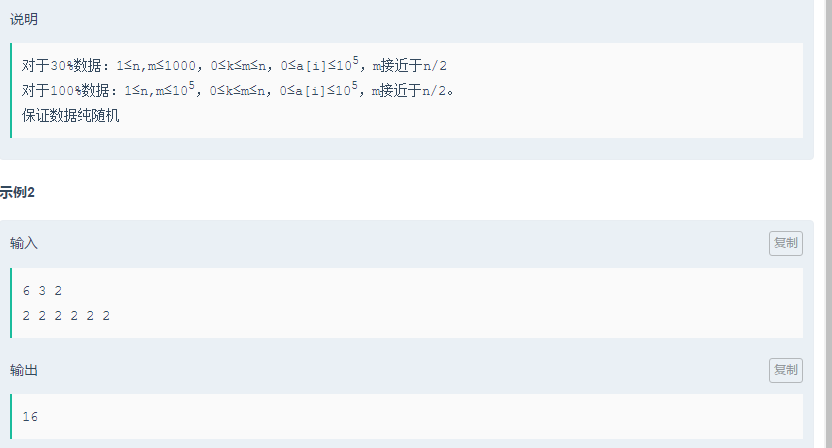
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1e5+10; 5 #define rep(i,first,last) for(int i=first;i<=last;i++) 6 #define dep(i,first,last) for(int i=first;i>=last;i--) 7 ll sumv[maxn<<3]; 8 ll cntv[maxn<<3]; 9 ll ans=0; 10 int n,m,k; 11 int a[maxn]; 12 13 void updata(int rt,int l,int r,int x,int val){ 14 if( l==r ){ 15 cntv[rt]+=val; 16 sumv[rt]+=(ll)l*val; 17 return ; 18 } 19 int mid=(l+r)>>1; 20 if( x>mid ) updata(rt<<1|1,mid+1,r,x,val); 21 else updata(rt<<1,l,mid,x,val); 22 sumv[rt]=sumv[rt<<1]+sumv[rt<<1|1]; 23 cntv[rt]=cntv[rt<<1]+cntv[rt<<1|1]; 24 } 25 ll query(int rt,int l,int r,int k){ 26 if( l==r ) return (ll)l*k; //这里若是return l*k;只能过90% 27 int mid=(l+r)>>1; 28 if( cntv[rt<<1]<k ) return sumv[rt<<1]+query(rt<<1|1,mid+1,r,k-cntv[rt<<1]); 29 else return query(rt<<1,l,mid,k); 30 } 31 32 int main() 33 { 34 scanf("%d%d%d",&n,&m,&k); 35 rep(i,1,n) scanf("%d",&a[i]); 36 rep(i,1,m) updata(1,0,maxn-5,a[i],1); 37 ans=query(1,0,maxn-5,k); 38 rep(i,m+1,n){ 39 updata(1,0,maxn-5,a[i-m],-1); 40 updata(1,0,maxn-5,a[i],1); 41 ans+=query(1,0,maxn-5,k); 42 } 43 printf("%lld\n",ans); 44 return 0; 45 }
题目链接:https://www.luogu.com.cn/problem/P1908
https://www.luogu.com.cn/problem/P3369
https://ac.nowcoder.com/acm/contest/900/B

