Codeforces Round #609 (Div. 2)E--K Integers(贪心+二分+树状数组+逆序对)
参考博客:https://blog.csdn.net/Q755100802/article/details/103664555
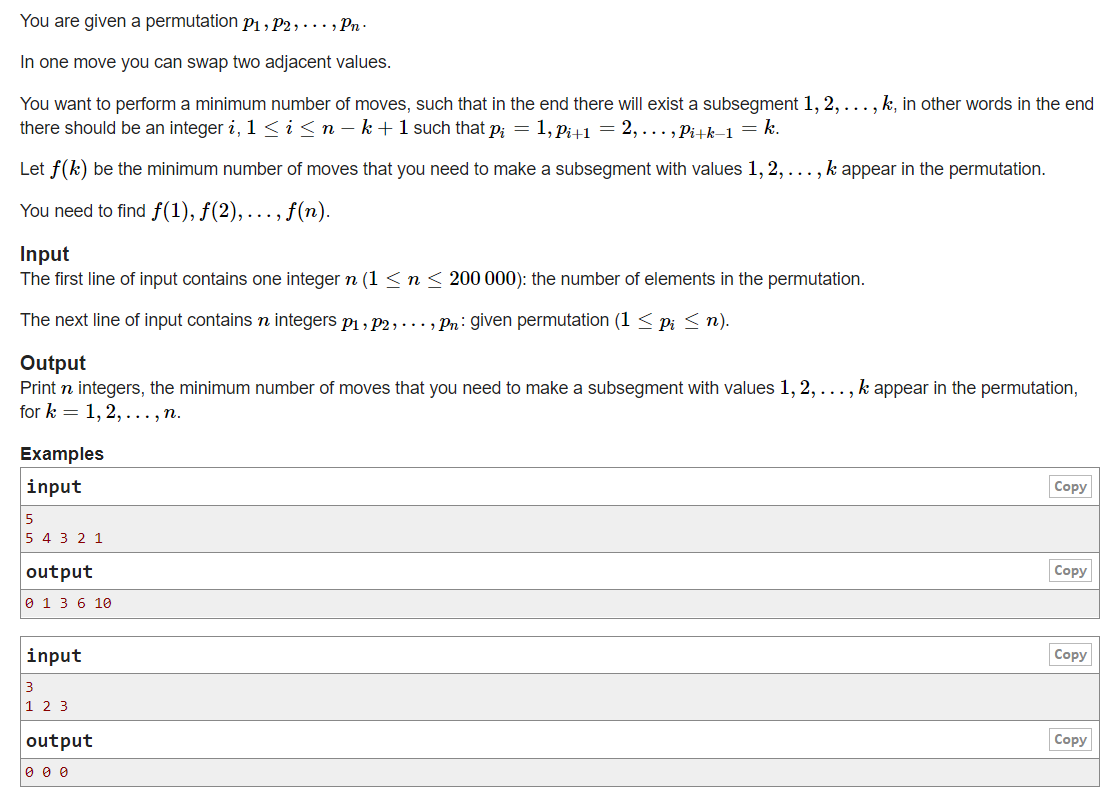
【题意】
给定一个1到n的排列,可以交换相邻的两个元素。
现在定义一个函数f(x),表示在原排列中,通过交换操作,形成一个1,2,3....x的排列的子串,需要的最小操作步骤。
子串意味着这个排列必须是相邻的。现在你需要求出f(1),f(2),f(3)......f(n)。
【分析】
在1~x这几个元素相邻的情况下,因为最后排列不存在逆序对,根据贪心思想,每一次操作都消除一对逆序对,这样每一次操作才不会浪费,所以,相邻的答案就是逆序对的个数。
不相邻的情况,如何移动才能使操作步数最少呢?答案应该是先将i个元素移动到一块儿,变成相邻的情况,再交换逆序对,这样才是最优的,(即答案为逆序对个数+往中间凑所移动的最小步数)因为这样操作,对于中间的每个不是当前排列的元素,他只会越来越往外面走,而不是混在i个元素中,造成操作的浪费。首先我们将所有元素移动到一块儿,移动到哪儿合适呢?位置mid应该是左右两边的元素个数尽量相等,这样我们就可以二分中间位置mid了;
然后,我们需要计算将元素尽量向中间点mid移动的花费,我们可以分为两部分:mid左边的部分,设个数为cnt(可以用树状数组O(log)求),假设cnt=2,如下图:

pos2移动到mid,需要花费mid-pos2;pos1移动到mid-1,需要花费mid-pos1-1;
如果还有pos3,pos4,花费也是同样计算的。假设位置pos之和为sum,花费为
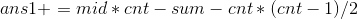
这就是左边的花费。
右边的同理,尽量往mid+1这个位置移动,假设右边的所有位置之和为sum,个数为cnt,花费为
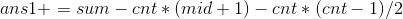
AC_Code:
1 #include <bits/stdc++.h> 2 typedef long long ll; 3 const int maxn=2e5+10; 4 using namespace std; 5 #define lowbit(i) ((i)&(-i)) 6 ll n,cnt,invnum,num,t; 7 ll sum1[maxn],sum2[maxn],pos[maxn]; 8 9 void updata(ll sum[],int i,int k){ 10 while( i<=n ){ 11 sum[i]+=k; 12 i+=lowbit(i); 13 } 14 } 15 16 ll getsum(ll sum[],int i){ 17 ll res=0; 18 while( i ){ 19 res+=sum[i]; 20 i-=lowbit(i); 21 } 22 return res; 23 } 24 25 ll bs(ll le,ll ri,ll num){ 26 ll mid; 27 while(le<=ri){ 28 mid=(le+ri)>>1; 29 if( getsum(sum1,mid)*2<=num ){ //注意我们是按顺序插入1~i,getsum(sum1,mid)就是问mid位置及以前的位置之前有几个数, 30 //我们要的情况是mid前后个数均分的情况 31 le=mid+1; 32 } 33 else ri=mid-1; 34 } 35 return le; 36 } 37 38 signed main() 39 { 40 scanf("%lld",&n); 41 invnum=0; 42 for(int i=1;i<=n;i++){ 43 scanf("%lld",&t); 44 pos[t]=i; 45 } 46 for(int i=1;i<=n;i++){ 47 updata(sum1,pos[i],1); 48 49 //pos[i]:i的位置,1~i【共有i个已经插入的数】的位置已经加1了,getsum(sum1,pos[i])i的位置的前面有几个加了1, 50 //也就是有几个比i小的数在i的前面,这几个数是不构成逆序数的 51 //那么剩下的就是i-query(pos[i])就是i所造成的逆序数 52 invnum+=(i-getsum(sum1,pos[i])); //求逆序数 53 updata(sum2,pos[i],pos[i]); 54 ll l=1,r=n; 55 ll mid=bs(l,r,i); //二分找位置 56 ll ans=0; 57 cnt=getsum(sum1,mid); //左边的个数 58 num=getsum(sum2,mid); //左边的位置和 59 ans+=invnum; 60 ans += mid*cnt-num-cnt*(cnt-1)/2; 61 62 cnt=i-cnt; //右边的个数 63 num=getsum(sum2,n)-num; //右边的位置和,前缀和思想 64 ans += num-cnt*(mid+1)-cnt*(cnt-1)/2; 65 printf("%lld ",ans); 66 } 67 printf("\n"); 68 return 0; 69 }


