棋盘染色法（一）

双色相邻染色法(国际象棋棋盘染色法)

原论文地址：http://www.doc88.com/p-1438088100243.html

这个染色法的基本构图如图

正如它的名字所言，是分析问题的奇偶本质。我们可以发现这种染色法得到的一个质。我们可以发现这种染色法得到的一个图像有以下几个特点:

(1)这张图具有高度的对称性， 平移还是旋转或是翻折，都无法改变它的性质。

(2)这张图总体来 说黑白格子的个数相等，关键的一点是，所有的黑格都只与白格相邻，同样所有的白格都只与黑格相邻。

(3)于是，在这张图中任何一条格子到格子之间的路径都经过几乎相同的黑白格数，至多相差一个

(4)在这张图内任取块以黑白格子的边界为边界的区域所包含的黑白格数也至多只相差一个

 

【双色染色法的应用】

问题一：一个5*5的房间网，相邻房间是相通的，问能否从箭头房间进入走遍整个房间网并且不重复的走入一个房间?

如图黑线就是一条不重复走入房间的路径。

 

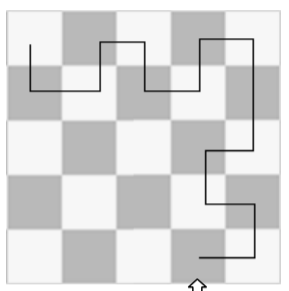
 这个问题的可以这样来考虑，5*5=25 是一个奇数，可以利用染色法尝试，由前面所推得的性质3得到:这条路房间网的话，黑白格数不是也只相差1吗?又由题意发现，起点在黑格，无论终点在黑格还是白格，都无法使白格数多于黑格数，于是，不存在这样的路径。有这个问题了以后，自然的想到了推广， 若是用1*2的小方块覆盖棋盘的话会有什么结果，巧的是，有一个著名的银行家曾经提出过类似的问题，下面的问题就来自那位银行家。

问题二：

一个8*8的格子纸，去掉对角两格,是否能用1*2的方块来覆盖它?

 

 

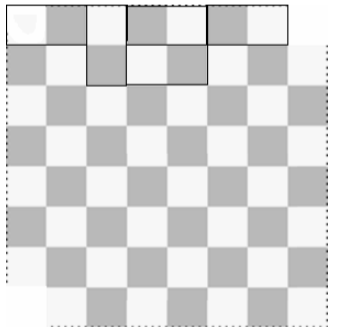
问题本质是1*2 的方块的覆盖，这启示我们问题基于的是奇偶性，我们把1*2 的方块盖于国际象棋棋盘之上后发现，由于黑的方格只与白的方格相邻，所以不管怎么放都会盖住以黑一白两块，这是一个重大的突破，我们数一下原问题中的黑白格数，发现黑格比白格少两个!于是该图形不可被1*2的方块覆盖。

这个结论同时也引发了新的问题，如果1*2的方块无法被覆盖的条件是黑白格数不等,如果是1*3的条状方块呢? 1*n 呢?这个问题就要用到多色染色法了。