Cooking Time

Cooking Time 

 

 

 

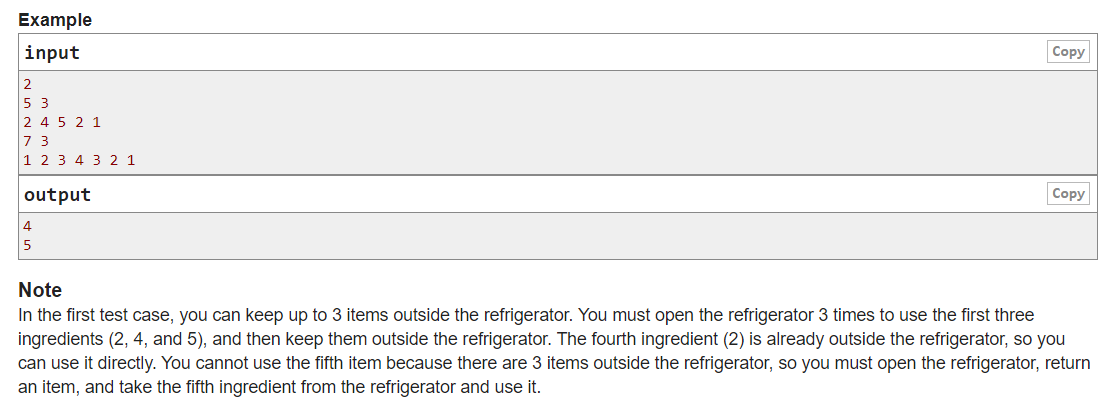
 题意： 有n种调料放在冰箱，你最多能把k种调料放外面，你每次打开冰箱，可以拿出一种调料，同时也可以放回去一种调料，也可以不放回。 每组输入案例第一行为n，k，第二行为n种调料的编号(从1到1e9),需要调料的顺序是输入的循序,输出是最少要打开多少次。

对于知道使用情况的置换算法，最优解是找一个最后需要使用的物品替换掉也就是，如果一个物品后面已经不需要用到，就要放回去了，当外面的物品达到了k个，此时某些情况我就得从外面中拿一个回去

思路：
离散化:看到a[i]比较大,而个数比较少,并且只需要知道相对编号就好,这时就想到了离散化
next数组下一个相同值在哪个位置;
last数组用来辅助next数组记录,一开始所有的last[a[i]]==inf,只要大于a[i]编号(a[i]的编号通过离散化只会最大从0~(n-1))就好了,所以这里我用了last[a[i]]=n;
inqueue数组用来判断是否物品在外面（即在队列中）
具体细节见代码

AC_Code

#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
int a[maxn],b[maxn],nxt[maxn],last[maxn],inqueue[maxn];

map<int,int>mp;
struct node{
    int nxt,id;
    bool operator < (const node &rhs ) const {
        return nxt<rhs.nxt;         //按下一次需要的"时间"从大到小排序
    }
};

int main()
{
    int t,n,k,ans;
    scanf("%d",&t);
    while( t-- ){
        ans=0;
        priority_queue<node>Q;
        memset(inqueue,0,sizeof(inqueue));
        mp.clear();

        int cnt=0;
        scanf("%d%d",&n,&k);
//        for(int i=0;i<n;i++){       //离散化
//            scanf("%d",&a[i]);
//            if( !mp.count(a[i])){
//                mp[a[i]]=cnt++;
//            }
//            a[i]=mp[a[i]];
//            last[a[i]]=n;
//        }

        for(int i=0;i<n;i++){       //这种离散化方式更快
            scanf("%d",&a[i]);
            b[i]=a[i];
        }
        sort(b,b+n);
        int reu=unique(b,b+n)-b;
        for(int i=0;i<n;i++){
            a[i]=lower_bound(b,b+reu,a[i])-b;
            last[a[i]]=n;
        }
        for(int i=n-1;i>=0;i--){    //设定next
            nxt[i]=last[a[i]];
            last[a[i]]=i;
        }

        for(int i=0;i<n;i++){
            if(inqueue[a[i]]){            //如果要拿出的物品已经外面有了，那就把这个也压入队列，
                                          //因为next值发生了变化，也要更新。这是a[i]最新的next值
                Q.push((node){nxt[i],a[i]});
                continue;
            }
            else if( k ){                //在外面的物品不够,直接拿出来
                Q.push((node){nxt[i],a[i]});
                inqueue[a[i]]=1;
                k--;
                ans++;
            }
            else{                       //在外面的物品够了,则要进行放进去,拿出来的操作
                node x=Q.top();
                Q.pop();
                inqueue[x.id]=0;
                Q.push((node){nxt[i],a[i]});
                inqueue[a[i]]=1;
                ans++;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}