Wall
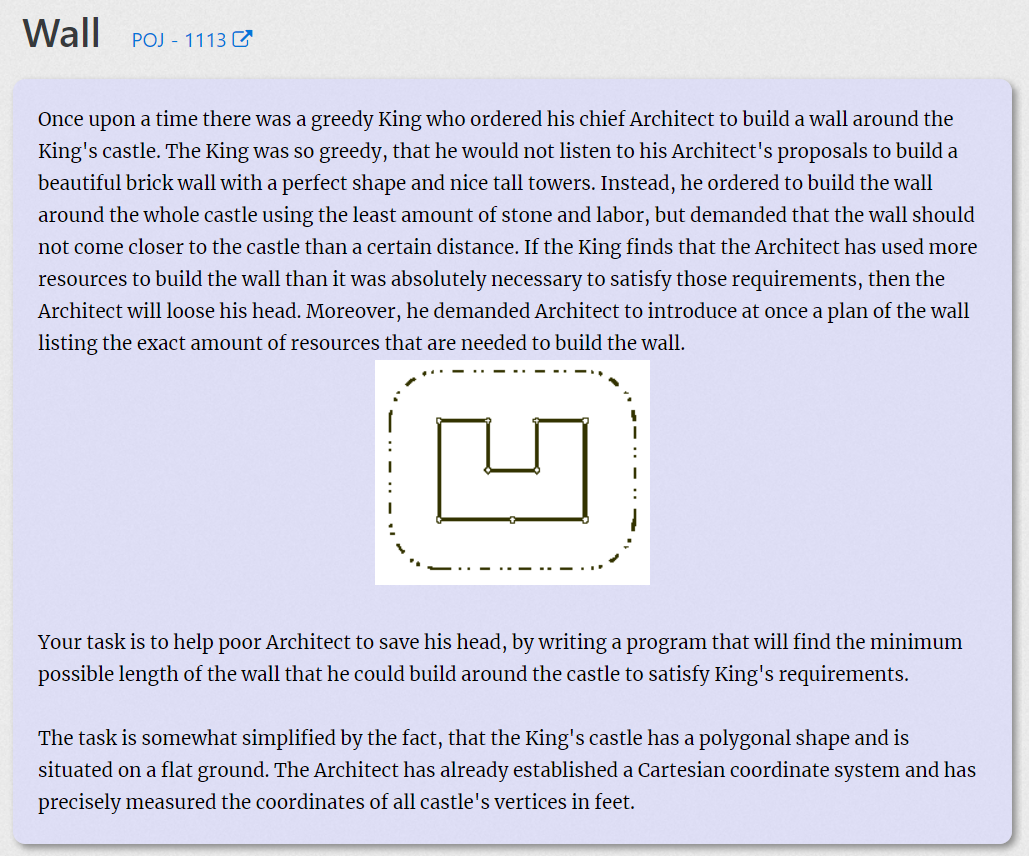

题目大意:给定n个点和一个距离L,要求围墙距离任意点的距离大于等于L,求出最小围墙长度。
最短的周长 = 凸包的周长 + 半径为L的圆的周长(顶点处加起来刚好为圆)
1 #include <cstdio> 2 #include <cstring> 3 #include <string> 4 #include <cmath> 5 #include <sstream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <set> 10 #include <map> 11 #include <algorithm> 12 #include <functional> 13 using namespace std; 14 const int maxn = 1010; 15 const double pi=acos(-1.0); 16 17 struct Point{ 18 double x,y; 19 bool extreme; 20 int succ; 21 }P[maxn]; 22 int ltl; 23 double ans; 24 25 bool cmp(const Point p1, const Point p2){ 26 if( p1.y==p2.y ) return p1.x<p2.x; 27 else return p1.y<p2.y; 28 } 29 30 bool Toleft(Point p, Point q, Point s){ 31 int area2 = p.x*q.y - p.y*q.x 32 + q.x*s.y - q.y*s.x 33 + s.x*p.y - s.y*p.x; 34 return area2>0;///左侧为真 35 } 36 37 int LTL(Point P[], int n){ 38 int ltl=0; 39 for(int k=1;k<n;k++){ 40 if( P[k].y<P[ltl].y || (P[k].y==P[ltl].y && P[k].x<P[ltl].x)){ 41 ltl=k; 42 } 43 } 44 return ltl; 45 } 46 47 double dis(int i,int j){ 48 double xx=P[i].x-P[j].x; 49 double yy=P[i].y-P[j].y; 50 return sqrt(xx*xx+yy*yy); 51 } 52 53 void Jarvis(Point P[], int n){ 54 for(int k=0;k<n; k++){ 55 P[k].extreme = false; 56 } 57 ltl=LTL(P,n); 58 int k=ltl; 59 do{ 60 P[k].extreme=true; 61 int s=-1; 62 for(int t=0;t<n;t++){ 63 if( t!=k && t!=s && (s==-1 || Toleft(P[k],P[s],P[t]))){ 64 s=t; 65 } 66 } 67 P[k].succ = s; 68 ans += dis(k,P[k].succ); 69 k=s; 70 }while(ltl!=k); 71 } 72 73 int main() 74 { 75 int n; 76 double r; 77 scanf("%d%lf",&n,&r); 78 for(int i=0;i<n;i++){ 79 scanf("%lf%lf",&P[i].x,&P[i].y); 80 } 81 ans = 0.0; 82 sort(P,P+n,cmp);///一定要排序 83 Jarvis(P,n); 84 // int k=ltl; 85 // do{ 86 // ans += dis(k,P[k].succ); 87 // k = P[k].succ; 88 // }while(k!=ltl); 89 90 ans += 2*pi*r; 91 printf("%.0f\n",ans); 92 return 0; 93 }
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 using namespace std; 7 typedef long long ll; 8 const int maxn=1100; 9 const double pi=acos(-1.0); 10 struct node{ 11 double x,y; 12 }p[maxn],a[maxn]; 13 int n,tot; 14 15 double dis(node a, node b){ 16 return hypot(a.x-b.x,a.y-b.y); 17 } 18 19 //return 正:p2在向量p0p1的左侧;return 负:p2在向量p0p1的右侧;return 0:三点共线 20 double multi(node p0,node p1,node p2){ 21 return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); 22 } 23 //极角排序:根据坐标系内每一个点与x轴所成的角,逆时针比较,按照角度从小到大排序 24 int cmp(node a, node b){ 25 int x=multi(a,b,p[0]); 26 if( x>0 || (x==0&& dis(a,p[0])<dis(b,p[0]))) return 1; 27 return 0; 28 } 29 30 void Graham(){ 31 int k=0; 32 for(int i=1;i<n;i++){ 33 if( p[i].y<p[k].y || (p[i].y==p[k].y&&p[i].x<p[k].x)) k=i; 34 } 35 swap(p[0],p[k]); 36 sort(p+1,p+n,cmp); 37 tot=2; 38 a[0]=p[0]; 39 a[1]=p[1]; 40 for(int i=2;i<n;i++){ 41 while( tot>1 && multi(p[i],a[tot-1],a[tot-2])>=0 ){//a[tot-2]在p[i]a[tot-1]的左侧或三点共线,则p[i]在a[tot-2]a[tot-1]的右侧,则a[tot-1]不是极点 42 tot--; 43 } 44 a[tot++]=p[i]; 45 } 46 } 47 48 int main() 49 { 50 // int t; 51 // scanf("%d",&t); 52 // while( t-- ){ 53 double r; 54 scanf("%d%lf",&n,&r); 55 for(int i=0;i<n;i++) scanf("%lf%lf",&p[i].x,&p[i].y); 56 Graham(); 57 double ans=0; 58 for(int i=0;i<tot-1;i++){ 59 ans+=dis(a[i],a[i+1]); 60 } 61 ans += dis(a[tot-1],a[0]); 62 ans += 2*pi*r; 63 printf("%.0f\n",ans); 64 // } 65 return 0; 66 }


