动态规划之四边形不等式优化

给出伪代码:(可以看出时间复杂度为O(n^3))
1 for(int len=1;len<=n;len++){///len为区间长度 2 for(int l=1;l<=n-len+1;l++){ 3 int r=l+len-1; 4 for(int k=l;k<r;k++){ 5 m[l][r]=min(m[l][r],m[l][k]+m[k+1][r]+w[l][r]); 6 } 7 } 8 }
以下介绍两个名词:区间包含的单调性:如果对于i≤i'< j≤j',有w(i',j)≤w(i,j'),那么说明w具有区间包含的单调性。
四边形不等式:如果对于i≤i'< j≤j',有w(i,j)+w(i',j')≤w(i',j)+w(i,j'),我们称函数w满足四边形不等式。
附图理解四边形不等式:

蓝线长和<=红线长和
以下介绍两个定理:定理一:如果上述的w函数同时满足区间包含单调性和四边形不等式性质,那么函数m也满足四边形不等式性质。

定理二:
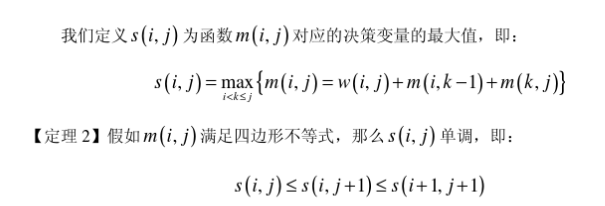
结论:

时间复杂度变为O(n^2)


