相似基因

相似基因

 

 

 

 

 

 

 

很好的题解

 

1.dp 基本思路

dp 题基本这么几个步骤：

 

1. 定义状态。
2. 写出状态转移式。
3. 根据状态转移式找出递推顺序。
4. 处理递推的边界。
5. 找出结果。

 

我讲解时不会就题论题，而是讲大部分黄绿难度的 dp 题的方法。

 

当然，dp 题十分灵活，不会看完这篇题解就会做，关键在于大量的练习。

 

2.状态定义

 

定义状态是 dp 最重要的步骤之一，状态定义得不好后面全都无法进行。

 

像这种线性动态规划，定义经常是“fi​ 表示前 i 个满足要求时的答案”。

 

因为这道题有两个串，很容易想到状态的定义是“fi,j​ 表示 a 串的前 i 个碱基和 b 串的前 j 个碱基的相似度”。

 

3.转移式

 

通常定义出状态之后转移式就十分好写了。转移式通常只需要考虑最后一点，比如这道题只用考虑最后一对碱基。

 

最后一对碱基只有以下3种可能：

 

1. 非空碱基和非空碱基。
2. 非空碱基和空碱基。
3. 空碱基和非空碱基。

 

注：空碱基和空碱基不能匹配。

 

去掉最后一对碱基，转化成规模更小的同样的问题，就是转移式的意义。易得如下转移式：

 

 

 

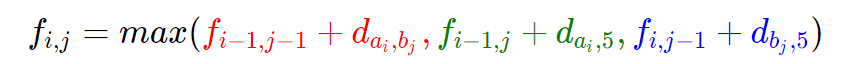
其中 di,j​ 表示编号为 i 的碱基和编号为 j 的碱基的相似程度，编号为5的是空碱基，ai​ 表示第一个基因的第 i 个碱基，b 表示第二个基因的第 i 个碱基。

 

其中红色代表第一种情况的转移，绿色代表第二种，蓝色代表第三种。

 

如果还不能明白，就看下面的图吧：

 

 

4.递推顺序

 

这步通常挺简单的，看看下标是变大还是变小。如果你要滚动数组的话（这题好像不能用滚动数组），递推顺序就会难一些。

 

显然，转移时下标不会变大，为了无后效性，应该从小到大递推。至于先枚举 i 还是 j，并不重要。

 

5.边界

 

递推顺序找到，边界就很容易找到了。

 

既然下标都是不变或变小，那边界就是至少有一个下标为0。如果一个下标为0，另一个下标不为0，上面3种转移只有一种有效，即：

 

 

 

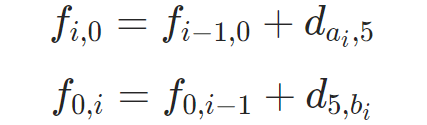
如果两个下标都为0，也就是 f0,0​，三个转移都会失效。我们应该按照定义赋给它值：0个碱基和0个碱基的相似度应为0。所以得到最后一个式子：

 

 

 

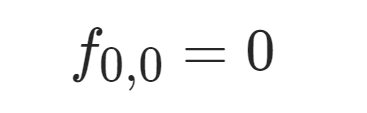
6.结果

 

这道题的结果很好找，就是，但是有些题的结果还得在多个数中找，比较麻烦。

 

7.实现

 

5个步骤的思维顺序如上，但是代码顺序略有不同，大概是这样的：

 

1. 状态定义。
2. 输入。
3. 递推边界。
4. 递推顺序。
5. 状态转移式。
6. 找出结果。

 

 

AC_Code

 

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdlib>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 205;
const int inf=0x3f3f3f3f;
const ll mod=1e9+7;

const int tab[6][6]={
    {0,0,0,0,0,0},
    {0,5,-1,-2,-1,-3},
    {0,-1,5,-3,-2,-4},
    {0,-2,-3,5,-2,-2},
    {0,-1,-2,-2,5,-1},
    {0,-3,-4,-2,-1,0}
};

int la,lb;
char sa[maxn],sb[maxn];
int a[maxn],b[maxn];
int dp[maxn][maxn];

int main()
{
    scanf("%d",&la);
    scanf("%s",sa);
    scanf("%d",&lb);
    scanf("%s",sb);
////    printf("%s",sa);
////    printf("%s",sb);
    for(int i=1;i<=la;i++){
        for(int j=1;j<=lb;j++){
            dp[i][j]=-inf;
        }
    }

    for(int i=1;i<=la;i++){
        if( sa[i-1]=='A') a[i]=1;
        if( sa[i-1]=='C') a[i]=2;
        if( sa[i-1]=='G') a[i]=3;
        if( sa[i-1]=='T') a[i]=4;
    }

    for(int i=1;i<=lb;i++){
        if( sb[i-1]=='A') b[i]=1;
        if( sb[i-1]=='C') b[i]=2;
        if( sb[i-1]=='G') b[i]=3;
        if( sb[i-1]=='T') b[i]=4;
    }

    dp[0][0]=0;
    for(int i=1;i<=la;i++){
        dp[i][0]=dp[i-1][0]+tab[a[i]][5];
    }
    for(int i=1;i<=lb;i++){
        dp[0][i]=dp[0][i-1]+tab[5][b[i]];
    }
    for(int i=1;i<=la;i++){
        for(int j=1;j<=lb;j++){
            dp[i][j]=max(dp[i-1][j-1]+tab[a[i]][b[j]],max(dp[i-1][j]+tab[a[i]][5],dp[i][j-1]+tab[5][b[j]]));
        }
    }
    printf("%d\n",dp[la][lb]);
    return 0;
}