战略游戏(树形DP入门）

题目链接：here

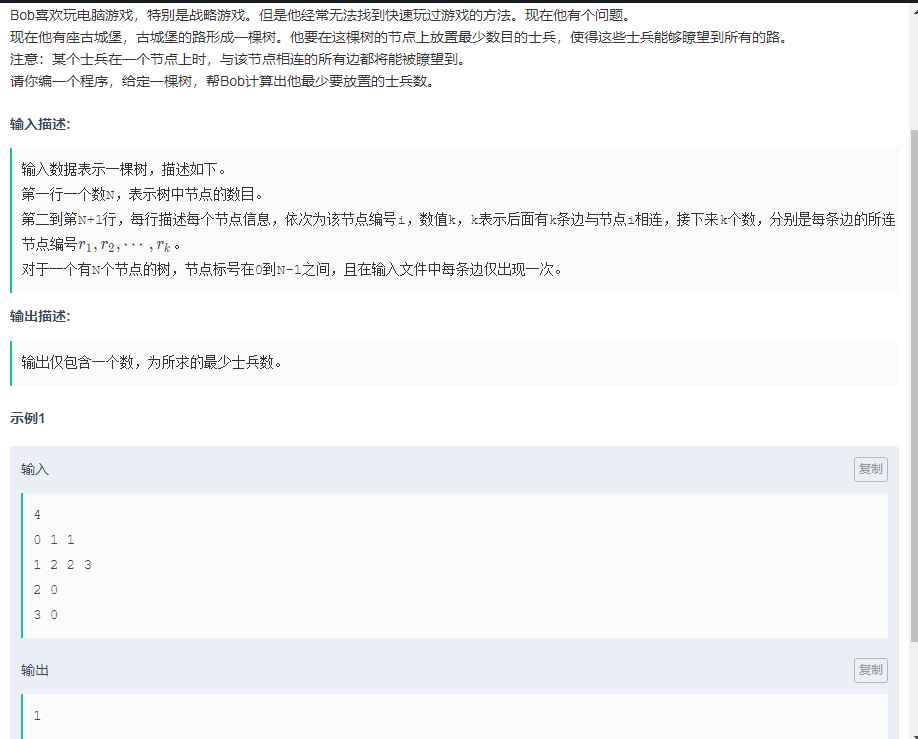
题目分析：

放置哨兵无非两种情况，放或不放，我们可以用dp[i][1]来表示第i个结点放置哨兵,dp[i][0]来表示第i个结点不放置哨兵,我们可以从上往下，从左往右来遍历树，所以这就用到了树形DP的知识，我们很容易知道，如果父亲结点没放哨兵，那么子结点肯定要放置哨兵，如果父亲放置了哨兵，那么子结点可以考虑放或者不放。所以很容易写出状态转移方程dp[v][1] += min(dp[u][1],dp[u][0]),dp[v][0] += dp[u][1]

和我的上一篇差不多：https://www.cnblogs.com/wsy107316/p/11319167.html

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1500+10;
const int mod = 1e9+7;
const int inf = 0x3f3f3f3f;


struct node{
    int to,nxt;
}e[maxn<<1];
int n;
int head[maxn];
int tot;
int dp[maxn][2];

void init(){
    memset(head,-1,sizeof(head));
    tot = 0;
}

void addedge(int u,int v){
    e[tot].to=v; e[tot].nxt=head[u]; head[u]=tot++;
}

void dfs(int u,int fa){
    for(int i=head[u];~i;i=e[i].nxt){
        int to=e[i].to;
        if( to==fa ) continue;
        dfs(to,u);
        dp[u][0] += dp[to][1];
        dp[u][1] += min(dp[to][1], dp[to][0]);
    }
}

int main()
{
    scanf("%d",&n);
    init();
    for(int i=1;i<=n;i++){
        int u, k; scanf("%d%d",&u,&k);
        for(int j=0;j<k;j++){
            int v; scanf("%d",&v);
            addedge(u,v);
            addedge(v,u);
        }
    }

    for(int i=0;i<=n;i++){
        dp[i][0] = 0;
        dp[i][1] = 1;
    }
    dfs(0,-1);
    int minn = inf;
    minn = min(dp[0][1], dp[0][0]);
    printf("%d\n",minn);
    return 0;
}