动态规划———最长公共子序列（LCS）

最长公共子序列+sdutoj2080改编：

http://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Contest/contestproblem/cid/2788/pid/2080

传送门： https://blog.csdn.net/sunshine_pb/article/details/21820159 

 

 

设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk}，

 

记：    Xk为序列X中前k个连续字符组成的子序列，

Yk为序列Y中前k个连续字符组成的子序列，

           Zk为序列Z中前k个连续字符组成的子序列，

 

显然有下式成立：

（1）若xm=yn，则zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列；

（2）若xm≠yn且zk≠xm，则Z是Xm-1和Y的最长公共子序列；

（3）若xm≠yn且zk≠yn，则Z是X和Yn-1的最长公共子序列。

 

  可见，两个序列的最长公共子序列包含了这两个序列的前缀序列的最长公共子序列。

要找出序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列，可按下述递推方式计算：

当xm=yn时，找出Xm-1和Yn-1的最长公共子序   列，然后在其尾部加上xm即可得到X和Y的最长公共子序列；

当xm≠yn时，必须求解两个子问题：找出Xm-1和Y的最长公共子序列以及Xm和Yn-1  的最长公共子序列，这两个公共子序列中的较长

者即为X和Y的最长公共子序列

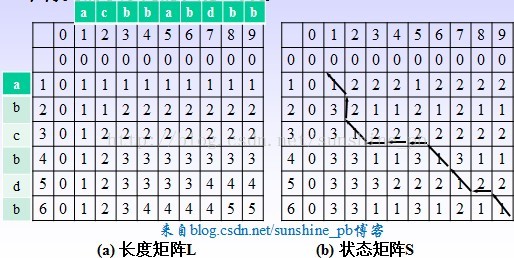
  设L[i][j]表示子序列Xi和Yj的最长公共子序列的长度，可得如下动态规划函数：

L[0][0] = L[i][0] = L[0][j] = 0           (1≤i≤m,1≤j≤n)

 

   L[i][j]只是记录子序列的长度，要打印得到X_m和Y_n具体的最长公共子序列，设二维表S[m+1][n+1]，其中S[i][j]表示在计算L[i][j]的过程中的搜索状态，并且有：

 

 

 

若S[i][j]=1，表明ai=bj，则下一个搜索方向是S[i-1][j-1]；

若S[i][j]=2，表明ai≠bj且L[i][j-1]≥L[i-1][j]，则下一个搜索方向是S[i][j-1]；

若S[i][j]=3，表明ai≠bj且L[i][j-1]＜L[i-1][j]，则下一个搜索方向是S[i-1][j]。

举例：序列X=(a,b,c,b,d,b)，Y=(a,c,b,b,a,b, d, b,b)，建立两个(m+1)×(n+1)的二维表L和表S，分别存放搜索过程中得到的子序列的长

度和状态。

下面代码为sdutoj2080改编代码：

/* */
# include <bits/stdc++.h>
using namespace std;

int CommonOrder( int len1, int len2, char x[], char y[], char z[]);
int L[501][501];
int S[501][501];
int main()
{
    char a[501], b[501], z[501];
    int i, t, len1, len2;
    while( gets(a) && gets(b) )
    {
        len1 = strlen(a);
        len2 = strlen(b);
        t = CommonOrder(len1, len2, a, b, z);
        printf("%d\n", t);
        for( i=1; i<=t; i++ )
        {
            printf("%c%c", z[i], i==t?'\n':' ');
        }
    }
    return 0;
}

int CommonOrder(int m, int n, char x[], char y[], char z[])
{
    int j, i, k;
    for( j=0; j<=n; j++ )
    {
        L[0][j] = 0;
    }
    for( i=0; i<=m; i++ )
    {
        L[i][0] = 0;
    }
    for( i=1; i<=m; i++ )
    {
        for( j=1; j<=n; j++ )
        {
            if( x[i-1]==y[j-1] )
            {
                L[i][j] = L[i-1][j-1]+1;
                S[i][j] = 1;
            }
            else if( L[i][j-1]>=L[i-1][j] )
            {
                L[i][j] = L[i][j-1];
                S[i][j] = 2;
            }
            else
            {
                L[i][j] = L[i-1][j];
                S[i][j] = 3;
            }
        }
    }
    i = m;
    j = n;
    k = L[m][n];
    while( i>=0 && j>=0 )
    {
        if( S[i][j]==1 )
        {
            z[k] = x[i-1];
            k--;
            i--;
            j--;
        }
        else if( S[i][j]==2 )
        {
            j--;
        }
        else
        {
            i--;
        }
    }
    return L[m][n];
}

算法分析：在算法中，

第一个for循环的时间性能是O(n)；

第二个for循环的时间性能是O(m)；

第三个循环是两层嵌套的for循环，其时间性能是O(m×n)；

第四个for循环的时间性能是O(k)，而k≤min{m,n}，所以，算法的时间复杂性是O(m×n)。