【NOIP2014】飞扬的小鸟

　　题目戳这里

　　70分是很裸的。

　　定义f[i][j]表示到了（i，j）位置最少戳的次数

　　有三种转移

　　●f[i][j]=min{f[i-1][j-k*x[i-1]]+k}--------------------------dp1

　　从（i，j-k*x）连戳k次跳到（i，j）

　　●f[i][j]=min(f[i][j],f[i-1][j+y[i-1]])-------------------------dp2

　　从（i，j+y）不戳掉到（i，j）

　　●if(j==m)f[i][j]=min(f[i][j],f[i-1][t]+(j-t)/x[i-1]+1) -----dp3 

　　t为 i-1处的任意合法位置

　　j在顶端，所以只要（i-1，t）合法可能从任意 t 跳到（i，j），因为碰到上界无法跳且不死

　　

　　复杂度O（NM^2） 一个稳稳的T

 

 

　　100分有一个小优化

　　这样思考：此题是可以过O（NM）的，而f[i][j]是必须要的，i和j必须枚举，那么我们k的枚举就必须被干掉。   

　　

　　

                     

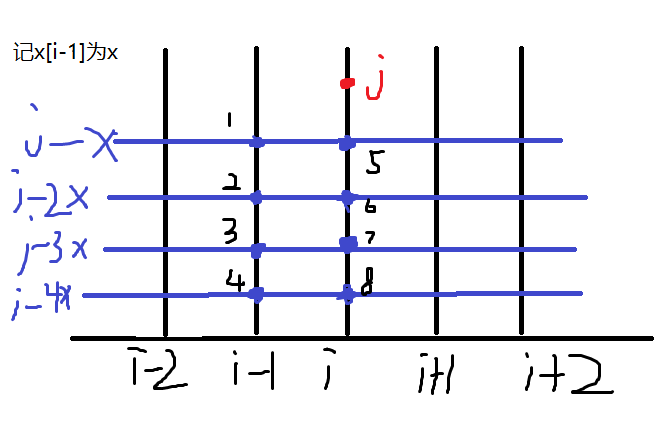
　　假设1,2,3,4,5,6,7,8号点和（i，j）点均合法

　　可见，对于上图

（i，j）点要由1,2,3,4号点转移过来

　　而5号点由2,3,4号点转移过来------->（i，j）可由5号点和1号点转移

　　   6号点由3,4号点转移过来------->5号点可由6号点和2号点转移

         7号点由4号点转移过来------->6号点可由7号点和3号点转移

　　f[i][j]可由f[i-1][j-x[i-1]]和f[i][j-x[i-1]]转移

　　道理很显然

　　f[i-1][j-k*x[i-1]]+k（k>=2）的信息全部存到了f[i][j-x[i-1]]中，k只用枚举1就行了

　　由于其他转移均为O（1）,所以不用优化

　　复杂度O（NM）　　

 

　　另外，若不能到达n，要求出能通过几根管子

　　这个其实很简单，只某一横坐标上所有合法点值均为inf，那么肯定不能到达此位置

　　记录个最远到达的横坐标，判断此横坐标前有几根管子就行了

 

　　写代码时有几点要注意

　　●先把所有向上跳的转移后再来转移向下降的

　　为什么？    因为我们毕竟不是（i，j-x[i-1]）点跳上来的

　　如果（i，j-x[i-1]）点最优转移是向下降，且（i，j）点最优转移是f[i][j-x[i-1]]

　　那么我们的f[i][j]=f[i][j-x[i-1]]是什么意思？先向下落了一点又跳上来？

　　这不符合游戏规则，所以要分开写。

　　  ●不只转移合法点，非法点（管子）也必须转移，因为它会存有（i-1，j-k*x[i-1]）k>=2的信息

　　●判断来源点是否合法

　　

　　　

　　至此，此题已解决

 

代码：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#define ll long long
#define N 1005
using namespace std;
int up[N*10],dn[N*10],x[N*10],y[N*10],f[N*10][N],n,m,k,ans2,ans1=0x3f3f3f3f;
int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=0;i<n;i++)scanf("%d%d",&x[i],&y[i]);
	for(int i=0;i<=n;i++)up[i]=m+1,dn[i]=0;
	for(int i=1;i<=k;i++){
		int p;scanf("%d",&p);
		scanf("%d%d",&dn[p],&up[p]);
	}
	memset(f,0x3f,sizeof(f));
	for(int i=0;i<=m;i++)f[0][i]=0;
	for(int i=1;i<=n;i++){
		int fg=0;
		for(int j=1;j<=m;j++){
			if(j-x[i-1]>0)f[i][j]=f[i][j-x[i-1]]+1;
			if(j-x[i-1]>dn[i-1]&&j-x[i-1]<up[i-1])      //dp1
			f[i][j]=min(f[i][j],f[i-1][j-x[i-1]]+1);
			if(j==m)for(int t=1;t<=j;t++)               //dp2
			if(t>dn[i-1]&&t<up[i-1])f[i][j]=min(f[i][j],f[i-1][t]+(j-t)/x[i-1]+1);
		}
		for(int j=dn[i]+1;j<up[i];j++){
			if(j+y[i-1]>dn[i-1]&&j+y[i-1]<up[i-1])      
			f[i][j]=min(f[i][j],f[i-1][j+y[i-1]]);
			if(f[i][j]<0x3f3f3f3f)fg=1;
		}
		if(fg)ans2=i;
		else break;
	}
	if(ans2!=n){
		int cnt=0;
		for(int i=0;i<=ans2;i++)if(up[i]!=m+1)cnt++;
		printf("0\n%d",cnt);
	}
	else{
		for(int i=dn[n]+1;i<up[n];i++)ans1=min(ans1,f[n][i]);
		printf("1\n%d",ans1);
	}
	return 0;
}