P5901 [IOI2009] regions 根号分治

根号分治

一个比较神奇的东西，就是你设置一个阈值，在小于等于这个阈值的时候，你有一个做法，在大于这个阈值的时候，你又有一种做法，两种做法合并起来的复杂度是可以接受的，就很神奇！

题意

一棵树，每个节点有颜色，每次询问两个颜色 \(r1\) \(r2\),问有多少在一条链上自上而下的点对颜色分别为 \(r1,r2\)。

分治

好！我们开始操作。
首先，肉眼观察出暴力做法：

• 定上面的点，统计子树的答案
• 定下面的点，统计祖先的答案

那么这两种方法，有什么不同呢？其实没有什么不同。
好，那我们来卡一卡这两种做法

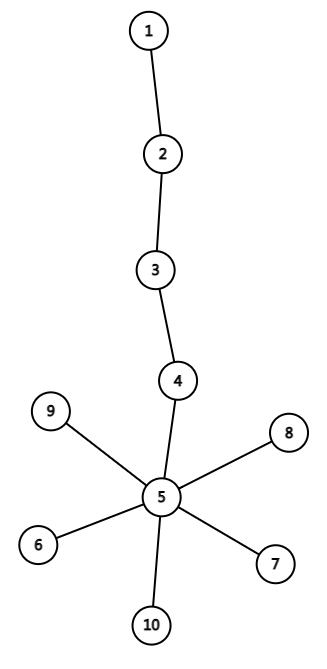
于是你有了这样的一个图。
假设那条链上省略 \(1e5\) 个节点
我们先令 \(1,2,3,4,5\) 对应颜色都为 \(1\)，其余均为对应编号，然后询问 \((1,9),(1,8),(1,7),(1,6)....\) 然后你发现，你的第一种方法炸了！
我们再令 \(1,2,3,4,5\) 对应颜色为编号，其余均为 \(1\)，然后询问 \((2,1),(3,1),(4,1)....\) 然后你发现，你的第二种方法炸了！

那我们就可以对 \(r2\) 进行一波分治，令阈值为 \(\sqrt{n}\):

• \(r2 \le \sqrt{n}\) 时，我们假设固定这样的一个 \(r2\)，采用固定下面的点向上面祖先统计答案的方法，那么最多有不超过 \(\sqrt{n}\) 次统计，因为是由 \(r2\) 向上开始找的，而我们对于这一个 \(r2\) 最多有 \(\sqrt{n}\) 种，也就是说对于这样的一种 \(r2\) 我们的操作上限次数控制在 \(\sqrt{n}\) 次，那么一共 \(q\) 次询问，总复杂度就是 \(O(q\sqrt{n})\) 的。
• \(r2 > \sqrt{n}\) 时，我们考虑采用定上面的点向下找的方法，那么我们假设定了当前的 \(r2\)，我们会固定整棵树的节点，也就是 \(n\) 个，分别统计，也就是说对于这一种 \(r2\) 的单操作 \(O(n)\)，而注意到 \(r2\) 的个数不会超过 \(\sqrt{n}\) 个，也就是说最多有 \(\sqrt{n}\) 种，所以这样的复杂度是 \(O(n\sqrt{n})\) 的。
• 总复杂度在 \(O(n\sqrt{n})\).

code :

#include<bits/stdc++.h>
using namespace std;
#define rep(a,b,c) for(int a=(b);a<=(c);++a)
template <typename T>
inline void read(T& x){
	   x = 0;int flag  = 0;char ch = getchar();
	   while(ch < '0' || ch > '9'){if(ch == '-')flag = 1;ch=getchar();}
	   while(ch >= '0' && ch <= '9')x=x*10+ch-'0',ch=getchar();
	   if(flag)x=-x;
}
template <typename T,typename ...Args>
inline void read(T& x,Args& ...tmp){read(x),read(tmp...);}
const int N = 2e5 + 5;
int n,r,m,cnt;
int a[N],num[N],ans[N];
vector<int>g[N];
vector<pair<int,int>>v1[N],v2[N];
#define pb push_back
void dfs1(int u){
	++num[a[u]];
	for(auto t : v1[a[u]]){
		ans[t.second] += num[t.first];
	}
	for(int v : g[u]){
		dfs1(v);	
	}
	--num[a[u]];
}
void dfs2(int u){
	for(auto t : v2[a[u]]){
		ans[t.second] -= num[t.first];
	}
	for(int v : g[u])dfs2(v);
	for(auto t : v2[a[u]])ans[t.second] += num[t.first];
	++num[a[u]];
}
int bcnt,id[N],s[500][N];
signed main(){
	read(n,r,m);
	int len = 640;
	read(a[1]);++num[a[1]];
	rep(i,2,n){
		int x;
		read(x,a[i]);
		++num[a[i]];
		g[x].pb(i);	
	}
	rep(i,1,r)if(num[i] > len)id[i] = ++bcnt;
	rep(i,1,m){
		int x,y;
		read(x,y);
		if(num[y] <= len)v1[y].pb({x,i});
		else{
			if(s[id[y]][x]){
				ans[i] = -s[id[y]][x];continue;	
			}
			s[id[y]][x] = i;
			v2[x].pb({y,i});
		}
	}
	rep(i,1,r)num[i] = 0;
	dfs1(1);
	rep(i,1,r)num[i] = 0;
	dfs2(1);
	rep(i,1,m)printf("%d\n",ans[i] > 0 ? ans[i] : ans[-ans[i]]);
}