如何理解汉诺塔的递归?
作者:魏闪
链接:https://www.zhihu.com/question/24385418/answer/107705695
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
这个时候,可以放张图了
链接:https://www.zhihu.com/question/24385418/answer/107705695
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
一个环:
Step1.将最大的环从A移动到C
A -> C
两个环:
Step1.把除了最大的环之外的环,从A移动到B
A -> B
Step2.将最大的环从A移动到C
A -> C
Step3.把除了最大的环之外的环,从B移动到C
B -> C
三个环:
Step1.把除了最大的环之外的环,从A移动到B
A -> C
A -> B
C -> B
Step2.将最大的环从A移动到C
A -> C
Step3.把除了最大的环之外的环,从B移动到C
B -> A
B -> C
A -> C
这个时候,可以放张图了

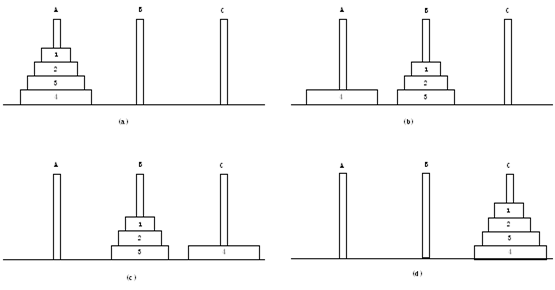
(a)是初始状态,也就是递归的起点,我们假设n=4, move(4,A,B,C)还是请参考现在最高的分的代码哈~写这个是帮助大家更清楚那个让人压力大的(“抽象”)两个字,哈哈
<这个函数要实现的功能是把n个环从A按照一定的规则,借助B,移动到C>
(b)是step1完成的时候的状态,已经将所有的n-1,这里也就是3个环从A挪到了B
<第一处递归,move(n-1,A,C,B) 这个函数要实现将n-1个环从A,借助C,移动到B>
(c)是step2,此时需要将第n个,也就是第四个最大的环从A挪到C
<move(1,A,B,C),或者干脆直接print("A -> C")>
(d)是step3,此时需要将B上面的n-1个环从B挪到C<第二处递归>
<第二处递归,move(n-1,B,A,C) 这个函数要实现将n-1个环从B,借助A,移动到C>
<这个函数要实现的功能是把n个环从A按照一定的规则,借助B,移动到C>
(b)是step1完成的时候的状态,已经将所有的n-1,这里也就是3个环从A挪到了B
<第一处递归,move(n-1,A,C,B) 这个函数要实现将n-1个环从A,借助C,移动到B>
(c)是step2,此时需要将第n个,也就是第四个最大的环从A挪到C
<move(1,A,B,C),或者干脆直接print("A -> C")>
(d)是step3,此时需要将B上面的n-1个环从B挪到C<第二处递归>
<第二处递归,move(n-1,B,A,C) 这个函数要实现将n-1个环从B,借助A,移动到C>



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步