数据结构之堆排序

堆排序

什么是堆?

• 完全二叉树
• 父节点都比子节点小或者都比子节点大

父节点和左子节点的关系?

i--2i+1

父节点和右节点的关系?

i--2i+2

排序之前

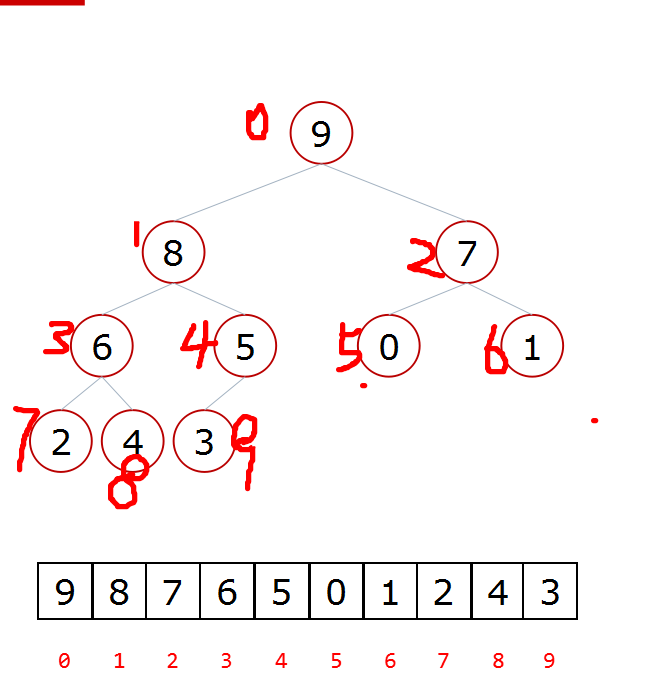
排序后的结果

def sift(data, low, high):
    """
    这是对树做一次调整保证其为大堆
    :param data: 这是数据列表
    :param low: 这是父节点
    :param high: 最后的子节点(这个树最左边或者最右边的子节点)
    :return:
    """
    i = low
    j = 2 * i + 1
    tmp = data[i]  # tmp是父节点
    while j <= high:  # 如果j不大于父节点的编号
        if j < high and data[j] < data[j + 1]:  # 说明还有右节点 且 判断右节点是否比左节点大
            j = j + 1  # 那就用右边的子节点跟父节点进行对比
        if tmp < data[j]:  # 父节点比子节点 的值小
            data[i] = data[j]  #把子节点的值放到父节点的位置
            i = j
            j = 2 * i + 1
        else:
            break
    data[i] = tmp  # 把要调整的值放到它不需要调整的位置


def heap_sort(data):
    """
    取值过程
    :param data: 数据列表
    :return:
    """
    n = len(data)
    for i in range(n // 2 - 1, -1, -1):  # n//2 -1 是最后一个子树的父节点
        sift(data, i, n - 1)  # 建立堆
    print(data)
    for i in range(n - 1, -1, -1):  # 堆底最后一个左节点---堆顶
        data[0], data[i] = data[i], data[0]  # 依次取出最大的值
        sift(data, 0, i - 1)  # 取一个最大值之后,做一次调整
    print(data)


if __name__ == '__main__':
    data = [9, 8, 7, 3, 6, 5, 0, 2, 1, 4]
    # data = [9,8,7,6,5,0,1,2,4,3]
    heap_sort(data)