UVA12075 Counting Triangles

组合计数难题,,,
主要思路是先用组合数算出任选3个点的所有情况, 然后再排除不成立的.
不成立的情况很明显就是三点共线. 对于三点共线的情况我们分为两类:

1. 三个点在一条水平或竖直直线上
2. 三个点在一条斜线上

在讨论情况之前, 我们先明确\(N\)和\(M\)指代的是水平直线的数量和竖直直线的数量, 不是题目给的格子数.

情况\(1\)很好处理, 直接\(N * C(M, 3) + M * C(N, 3)\)就好,,,
对于情况2, 首先要知道一个结论 :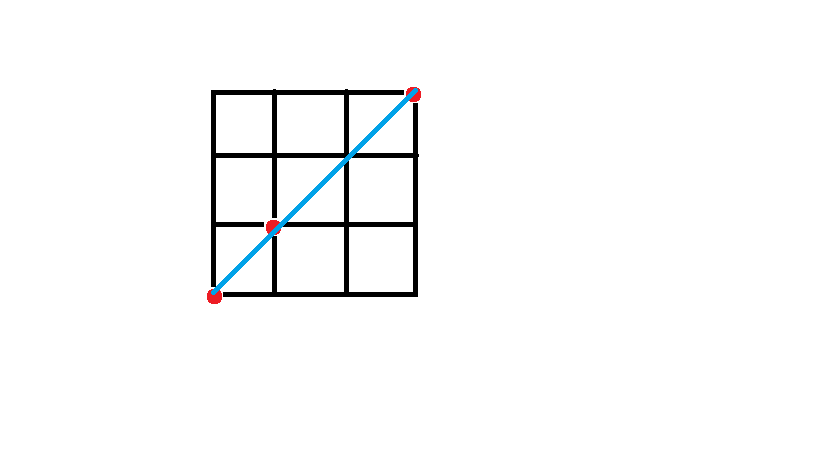
如图, 这样的一类 两个端点在 \((1, 1)\) 和 \((N, M)\) 上 的三点共线的个数是 \(gcd(N - 1, M - 1) - 1\).

你问我为什么, 肥肠爆芡, 我不太清楚, 请参考 这里.
有了这个结论, 就可以用算出在 \(N *　M\) 的矩阵内有多少的 从左下到右上 的三点共线.
在我的代码里, 第一次循环求sum是为了算出三点共线的个数, 第二次是为了前缀和统计答案.
记得最后统计的时候也要减去 从左上到右下 的三点共线, 所以要 \(* 2\).

#include <cstdio>
#include <cstring>
#include <cassert>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1e3 + 10;

int N, M;
int gcd(int a, int b){return b ? gcd(b, a % b) : a;}

inline ll C(int n, int k){
	if(k > n) return 0;
	ll tmp = 1;

	for(int i = 0; i < k; i++) 
		tmp *= 1LL * (n - i), tmp /= 1LL * (i + 1);
	return tmp;
}

ll sum[MAXN][MAXN];

int main(){
	// freopen("12075.in", "r", stdin);
	// freopen("12075.out", "w", stdout);
	for(int i = 2; i <= (int) 1e3; i++)
		for(int j = 2; j <= (int) 1e3; j++) 
			sum[i][j] = (gcd(i, j) - 1) + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];

	for(int i = 2; i <= (int) 1e3; i++)
		for(int j = 2; j <= (int) 1e3; j++) 
			sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];

	int t = 0;
	while(cin>>N>>M, N + M){
		++M, ++N;
		printf("Case %d: ", ++t);
		cout<<C(N * M, 3) - 1LL * N * C(M, 3) - 1LL * M * C(N, 3) - (sum[N - 1][M - 1] << 1)<<endl;
	}
	return 0;
}