kmp
参考:https://www.cnblogs.com/tangzhengyue/p/4315393.html
求解next数组:
下面说说面试的时候,给一个字符串,要你写出它的Next数组,应该怎么写:

①:先对每一位左边的子串求出最大前后缀串的长度,作为初始的Next数组
②:因为第一位失配时需要移动i,因此赋值为-1
③:P[3] == A, Next[3] == 0, P[0] == A; 所以P[3] == P[0], (移动过去后还是失配,需要继续移动),优化Next[3]为Next[0],即-1
④:同理优化Next[10]为Next[0],即-1
⑤:同理优化P[14],P[15],P[16]
暴力解法:
模式串: Pattern 文本串: Text
1 int match(string text,string pattern){
2 size_t n = text.size(), i=0;
3 size_t m = pattern.size(), j=0;
4 while(j<m && i<n){
5 if(text[i] == pattern[j]){ i++;j++;}
6 else { i=i-j+1; j=0; }
7 }
8 if(j==m) return i-j; //匹配成功
9 else return -1; //匹配失败
10 }
KMP
next数组其实就是查找模式串中每一位前面的子串的前后缀有多少位匹配,从而决定j失配时应该回退到哪个位置。
KMP算法与BF算法的区别就在于KMP算法巧妙的消除了指针i的回溯问题,只需确定下次匹配j的位置即可,使得问题的复杂度由O(mn)下降到O(m+n)。
在KMP算法中,为了确定在匹配不成功时,下次匹配时j的位置,引入了next[]数组,next[ j ], 即在P[0,j)中,最大自匹配的真前缀和真后缀的长度。
对于next[]数组的定义如下:
1) next[ j ] = -1 j = 0
2) next[ j ] = max(k): 0<k<j P[0...k-1]=P[j-k,j-1]
3) next[ j ] = 0 其他
P a b a b a
j 0 1 2 3 4
next -1 0 0 1 2
即next[j] = k > 0时,表示P[0,k-1] = P[j-k,j-1] 真前缀和真后缀的长度相等
因此KMP算法的思想就是:在匹配过程称,若发生不匹配的情况,如果next[j]>=0,则目标串的指针i不变,将模式串的指针j移动到next[j]的位置继续进行匹配;若next[j]=-1,则将i右移1位,并将j置0,继续进行比较。


理解next数组:
KMP的next数组简单来说,假设有两个字符串,一个是待匹配的字符串strText,一个是要查找的关键字strKey。现在我们要在strText中去查找是否包含strKey,用i来表示strText遍历到了哪个字符,用j来表示strKey匹配到了哪个字符。
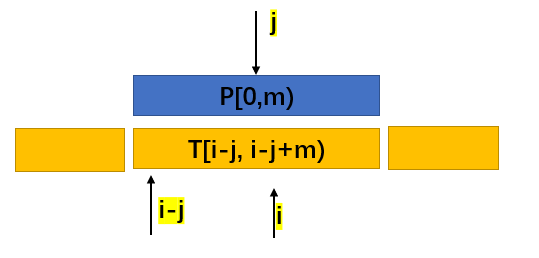
如果是暴力的查找方法,当strText[i]和strKey[j]匹配失败的时候,i和j都要回退,然后从i-j的下一个字符开始重新匹配。
而KMP就是保证i永远不回退,只回退j来使得匹配效率有所提升。它用的方法就是利用strKey在失配的j为之前的成功匹配的子串的特征来寻找j应该回退的位置。而这个子串的特征就是前后缀的相同程度。
所以next数组其实就是查找strKey中每一位前面的子串的前后缀有多少位匹配,从而决定j失配时应该回退到哪个位置。
我知道上面那段废话很难懂,下面我们看一个彩图:

这个图画的就是strKey这个要查找的关键字字符串。假设我们有一个空的next数组,我们的工作就是要在这个next数组中填值。
下面我们用数学归纳法来解决这个填值的问题。
这里我们借鉴数学归纳法的三个步骤(或者说是动态规划?):
1、初始状态
2、假设第j位以及第j位之前的我们都填完了
3、推论第j+1位该怎么填
初始状态我们稍后再说,我们这里直接假设第j位以及第j位之前的我们都填完了。也就是说,从上图来看,我们有如下已知条件:
next[j] == k;
next[k] == 绿色色块所在的索引;
next[绿色色块所在的索引] == 黄色色块所在的索引;
这里要做一个说明:图上的色块大小是一样的(没骗我?好吧,请忽略色块大小,色块只是代表数组中的一位)。
我们来看下面一个图,可以得到更多的信息:

1.由"next[j] == k;"这个条件,我们可以得到A1子串 == A2子串(根据next数组的定义,前后缀那个)。
2.由"next[k] == 绿色色块所在的索引;"这个条件,我们可以得到B1子串 == B2子串。
3.由"next[绿色色块所在的索引] == 黄色色块所在的索引;"这个条件,我们可以得到C1子串 == C2子串。
4.由1和2(A1 == A2,B1 == B2)可以得到B1 == B2 == B3。
5.由2和3(B1 == B2, C1 == C2)可以得到C1 == C2 == C3。
6.B2 == B3可以得到C3 == C4 == C1 == C2
上面这个就是很简单的几何数学,仔细看看都能看懂的。我这里用相同颜色的线段表示完全相同的子数组,方便观察。
接下来,我们开始用上面得到的条件来推导如果第j+1位失配时,我们应该填写next[j+1]为多少?
next[j+1]即是找strKey从0到j这个子串的最大前后缀:
#:(#:在这里是个标记,后面会用)我们已知A1 == A2,那么A1和A2分别往后增加一个字符后是否还相等呢?我们得分情况讨论:
(1)如果str[k] == str[j],很明显,我们的next[j+1]就直接等于k+1。
用代码来写就是next[++j] = ++k;
(2)如果str[k] != str[j],那么我们只能从已知的,除了A1,A2之外,最长的B1,B3这个前后缀来做文章了。
那么B1和B3分别往后增加一个字符后是否还相等呢?
由于next[k] == 绿色色块所在的索引,我们先让k = next[k],把k挪到绿色色块的位置,这样我们就可以递归调用"#:"标记处的逻辑了。
由于j+1位之前的next数组我们都是假设已经求出来了的,因此,上面这个递归总会结束,从而得到next[j+1]的值。
我们唯一欠缺的就是初始条件了:
next[0] = -1, k = -1, j = 0
另外有个特殊情况是k为-1时,不能继续递归了,此时next[j+1]应该等于0,即把j回退到首位。
即 next[j+1] = 0; 也可以写成next[++j] = ++k;
public static int[] getNext(String ps)
{
char[] strKey = ps.toCharArray();
int[] next = new int[strKey.length];
// 初始条件
int j = 0;
int k = -1;
next[0] = -1;
// 根据已知的前j位推测第j+1位
while (j < strKey.length - 1)
{
if (k == -1 || strKey[j] == strKey[k])
{
next[++j] = ++k;
}
else
{
k = next[k];
}
}
return next;
}
现在再看这段代码应该没有任何问题了吧。
优化:
细心的朋友应该发现了,上面有这样一句话:
(1)如果str[k] == str[j],很明显,我们的next[j+1]就直接等于k+1。用代码来写就是next[++j] = ++k;
可是我们知道,第j+1位是失配了的,如果我们回退j后,发现新的j(也就是此时的++k那位)跟回退之前的j也相等的话,必然也是失配。所以还得继续往前回退。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号