leetcode 60. 第k个排列,回溯以及剪枝
给出集合 \([1,2,3,…,n]\),其所有元素共有 \(n!\) 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
"123"
"132"
"213"
"231"
"312"
"321"
给定 \(n\) 和 \(k\),返回第 \(k\) 个排列。
说明:
- 给定 \(n\) 的范围是 \([1, 9]\)。
- 给定 \(k\) 的范围是 \([1, n!]\)。
思路讲解
本体是典型的回溯模型,全排列问题经常使用到回溯的技巧。但是本题仅仅让我们返回第k个序列,而不是全排列的全体,这样的话,我们就得在回溯模型的基础上,进行剪枝,得到所需要的那个答案。
根据回溯的思想,我们每次都要进行一次选择,然后递归下去。起初我们构建我们的选择数组,我们用一个vector 容器承接我们所有的选择,vector push 进去\(1\)到\(n\)。这个数组跟随我们的递归不断深入下去,我们在每一层的递归中从这个vector 选择容器中,选出我们应该选的那个元素,然后再将这个元素利用erase 接口消除掉。等到这个容器没有可供选择的选项时候,那么我们就return 函数返回。
那么问题就来了,我们应该怎样选择我们需要的那个数组呢。
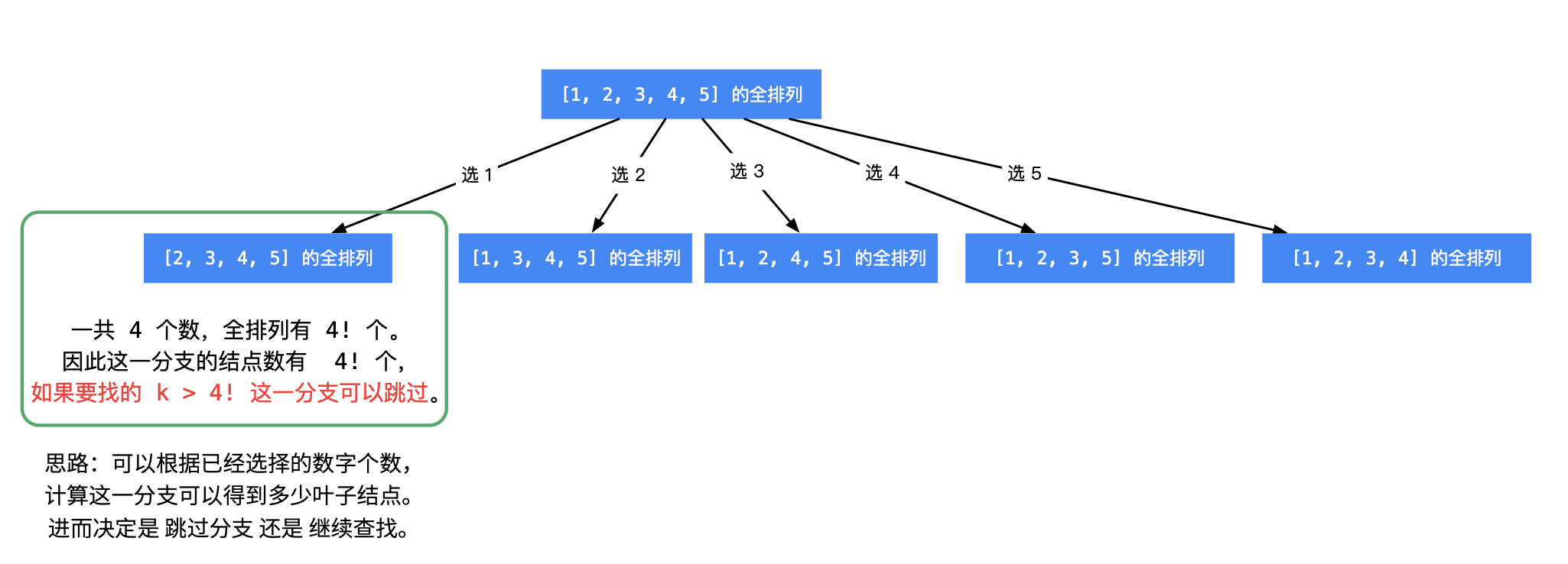
- 我们面对一个选择数组,数组大小为\(n\),那么这个选择数组一共有 \(n!\)排列的结果,我们也明白我们需要选择第\(k\)大的排列结果。
- 因为我们的选择数组的选项的大小是从小到大的,所以如果我们选了第一个选项,那么我们在此基础上所做的结果,最大也就 (n-1)!大的序列,利用这个特性我们进行剪枝
剪枝的逻辑
for(int i = 0; i < choose.size(); i++){
if ( k > Factorial(choose.size()-1)){
k = k - Factorial(choose.size()-1);
# 我们不在做个选择了,那么我们在下一个选择中看寻找 第 k - Factorial(choose.size()-1)大小的选项
continue;
}else{
break;
# 找到这个选项,这个选项为第i项,我们break, 跳出for 循环
}
}
具体代码
class Solution {
private:
long jiecheng(int n){
if (n == 0 || n == 1)
return 1;
long res = 1;
for(int i = 1; i <= n; i++){
res = res * i;
}
return res;
}
private:
string res;
public:
string getPermutation(int n, int k) {
vector<int> choose;
for(int i = 1; i <= n; i++){
choose.push_back(i);
}
dfs(choose, k);
return res;
}
void dfs(vector<int>& choose, int& k){
if (choose.empty()){
return;
}
int choose_size = choose.size();
int i;
for(i = 0; i < choose.size(); i++){
if ( k > jiecheng(choose_size -1)){
k = k - jiecheng(choose_size -1);
continue;
}
break;
}
int make_choose = choose[i];
res = res + to_string(make_choose);
choose.erase(choose.begin() + i);
dfs(choose, k);
}
};

