流加密的密文解密

流加密的密文解密

解密目标

给出十篇加密的样例密文，求解密一篇特定的密文

解密前提

1. 全部密文使用同一Key加密
2. 加密的方法只是简单的异或操作
3. 原文绝大多数的内容都是以字母和空格为主

解密过程分析

首先，这些加密方式都是异或加密，使用的是同一个Key。我们从异或加密的一些方法进行入手，异或有以下的特征。

公式一：

\[(A \otimes C) \otimes (B \otimes C) = A \otimes B \]

公式二：

\[(A \otimes B) \otimes A = B \]

从上述公式我们可以得出一些推论

\[(原文_1 \otimes 密钥) \otimes (原文_2 \otimes 密钥) = 原文_1 \otimes 原文_2 = 密文_1 \otimes 密文_2 \]

\[(原文 \otimes 密钥) \otimes 原文 = 密钥 = 密文 \otimes 原文 \]

从这个推论我们可以问题简化为，只需要知道原文和对应的密文，也就能知道了密钥，最后再用密钥异或待解密的密文，就能反向得到其对应的原文了。

现在问题就变成了，如何知道密文对应的原文？

由于原文绝大多数的内容都是以字母和空格为主，所以可以利用空格ASCII码异或的一个特点进行入手。先分析一下ASCII码：

Char	ASCII code	Hex
Space	32	00100000
a~z	97~122	01100001~01111010
A~Z	65~90	01000001~01011010

因此，

\[Space \otimes alpha = 01XXXXXX \]

\[Alpha \otimes alpha = 00XXXXXX \]

这个推论表明了，在大部分情况下，如果异或得到的结果是字母，则双方应该一方是空格，另一方是对应字母的大小写。(特殊情况为，标点符号的ASCII码为001XXXXX，效果等同于space，只是不能对应大小写转换，这就是这次实验结果的干扰项，可以看到有时候的确解出来了原文的字母，但是原文的字母明显是错的，不符合英文语法)

因此，找到空格就约等于破解了Key。

解密流程

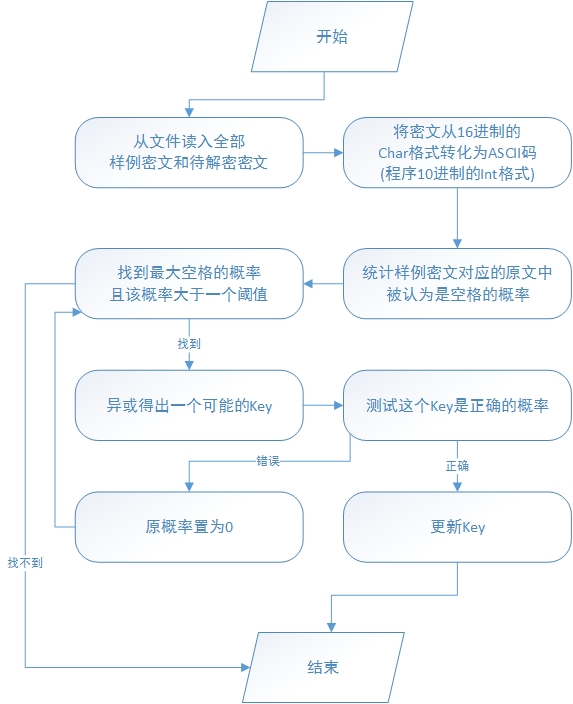
说明

空格的概率：某一篇的特定一位和其余的各篇异或操作，如果结果是字母，则认为它是空格的概率提高。由于只需要比较大小，程序中没有除以总的篇数，仅仅是比较分子大小。

阈值的选择：在这里我选择的阈值是至少两篇异或得出字母。

Key正确的概率：大量实验结果表明，50%是最好的判决点！再次声明，这个50%不是随便选的，是经过了大量的实验结果表明的，我也不知道它为什么就是50%，显得我很不专业。

程序结构

封装了一个解密类，用户需要调用addCiphertext()方法添加样例密文，添加越多，解密效果越好；然后调用decrypt()方法即可完成解密工作。getKey()方法和printKey()方法可以查看Key，如果有待解密的密文，使用addTargetCiphertext()方法添加后调用decryptTarget()即可解密，解密效果根据样例密文决定。

封装了一个单词拼写类，但这不是主要实验内容，使用了KMP搜索算法中的替换法则。

主要函数解析

void DecryptHelper::decryptKeyAtPosition(int position) {
	int maxCiphertext = ciphertextInt.size();
	int *spaceRatio = new int[maxCiphertext];
	int maxSpaceRatio = 0, maxSpaceRatioIndex = -1;
	// Statistics the space ratio for every ciphertext
	for (int i = 0; i < maxCiphertext; i++) {
		spaceRatio[i] = 0;
		if (position < ciphertextInt[i].size()) {
			int firstChar = ciphertextInt[i][position];
			for (int j = 0; j < ciphertextInt.size(); j++) {
				if (position < ciphertextInt[j].size() && j != i) {
					int secondChar = ciphertextInt[j][position];
					if (isalpha(firstChar ^ secondChar)) {
						spaceRatio[i]++;
						if (spaceRatio[i] >= 2 && spaceRatio[i] > maxSpaceRatio) {
							maxSpaceRatio = spaceRatio[i];
							maxSpaceRatioIndex = i;
						}
					}
				}
			}
		}
	}
	// Try to update the key
	while (maxSpaceRatioIndex != -1) {
		// Test if it is a real SPACE char
		int tryKey = ciphertextInt[maxSpaceRatioIndex][position] ^ SPACE;
		if (testKeyAtPosition(tryKey, position)) {
			key[position] = tryKey;
			break;
		}
		// Find another maxSpaceRatio key
		spaceRatio[maxSpaceRatioIndex] = 0;
		maxSpaceRatio = 0, maxSpaceRatioIndex = -1;
		for (int i = 0; i < maxCiphertext; i++) {
			if (spaceRatio[i] >= 2 && spaceRatio[i] > maxSpaceRatio) {
				maxSpaceRatio = spaceRatio[i];
				maxSpaceRatioIndex = i;
			}
		}
	}
	
	delete [] spaceRatio; 
}

bool DecryptHelper::testKeyAtPosition(int tryKey, int position) {
	int textCount = 0, alphaCount = 0;
	for (int i = 0; i < ciphertextInt.size(); i++) {
		if (position < ciphertextInt[i].size()) {
			textCount++;
			if (isalpha(ciphertextInt[i][position] ^ tryKey)) {
				alphaCount++;
			}
		}
	}
	if (alphaCount * 2 > textCount) {
		return true;
	}
	return false;
}

运行结果

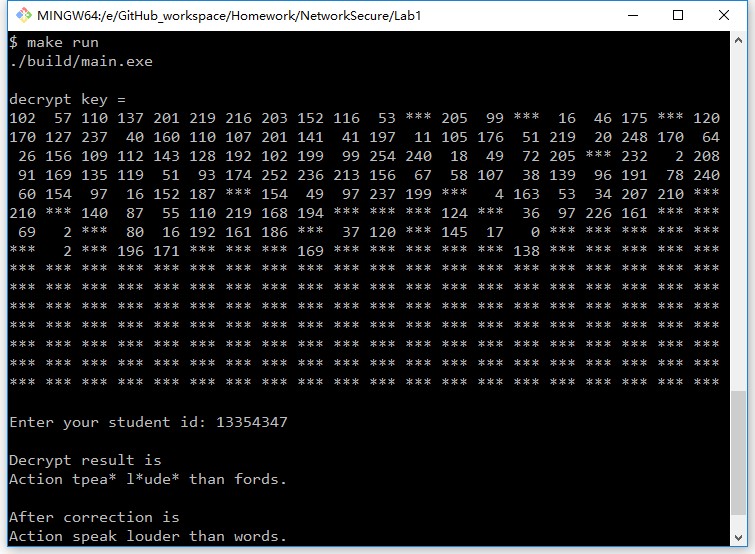
Key的长度我声明为300，因此后面会有比较多的*是因为没有这么长的样例密文来求解。破解率为：26/31=0.8387=83.87%，尽管不尽如意，但是已经能够通过英文语法规则来获知真正的内容。单词拼写检查设置为最多替换两个字符，再多了也没有意义，在80%+的破解率下运行良好。

一些心得

本次实验是关于密码破解的实验。根据上文描述的破解原理，我们可以得出一些结论，使用同一个Key加密原文的，会使得密文更容易被破解。根据统计特征，正常的英文文章中，字母的出现概率中会比非字母出现的概率多很多，因此，加密的密文越多，那么就越符合统计学特征，也就越容易被找到一个空格破解该位对应的Key。

下面来讨论一下课件上的三个问题：

• 许多空格问题
  这其实是由算法决定的，如果算法的思路是仅仅找到三个字符，一个是空格两个字母的话，能够很好的解决这一问题。但是，这个问题出现是小概率事件，一般情况下的解密效果会变差，所以多空格程序会认为找不到破解Key的关键，因为找到的决策是异或出现字母。

• 没有空格问题
  这个问题我觉得没有什么讨论的意义，连空格都没有，只能说解不出来好吧。哪怕刚刚好两个字符异或得到是字母，但是你会发现，最后解密的效果都是错的[手动笑脸]。

• 其他字符问题
  上文的讨论中我也已经提到了，标点符号的ASCII码是001XXXXX，异或字母的结果还是字母，所以能够在一定程度上影响解密效果。但是，符号的出现概率还是相对比较小，而且经过了测试函数对这个可能的Key进行过滤处理，能够在一定程度上消除这个影响，从而更好地解密。

最后，这次实验中学会了流加密的核心内容并得到了实践，我觉得流加密中也可以做交换位置这种操作来增加加密的效果，或者是用一个特定的字符替换全部的空格再加密，能够大大地提高加密效果，也就更加不容易被破解（但这样会大大提高我们的实验难度，我还是匿了。

附录

• build
  • main.exe （可执行程序）
• ciphertexts
  • multi-ciphertext.txt （样例密文）
  • multi-targetCiphertext.txt （待解密密文）
• result
  • final.txt （10篇待解密密文解密出来的原文）
• model
  • small.txt （正确单词的单词库）
• DecryptHelper.h （解密类声明）
• DecryptHelper.cpp （解密类实现）
• main.cpp （主函数）
• Makefile （编译文件）
• README.md （程序说明）

传送门：下载