树 总结

　特殊树

　　平衡二叉树（AVL树）：

　　平衡二叉树又称为AVL树，是一种特殊的二叉排序树。其左右子树都是平衡二叉树，且左右子树高度之差的绝对值不超过1。

　　由于过于平衡，在插入删除时需要大量旋转操作的，时间复杂度较高。

　　红黑树：

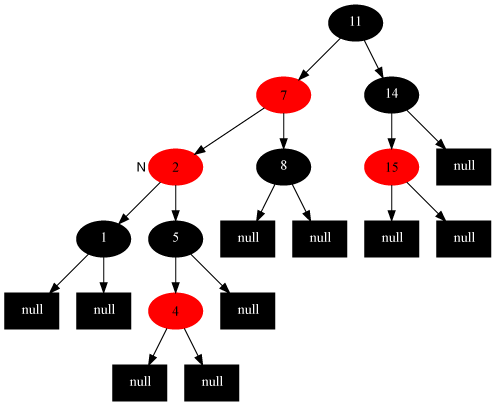
　　是一种二叉查找树，弱平衡二叉树，红黑树确保没有一条路径会比其他路径长出两倍。插入最多两次旋转，删除最多三次旋转，最坏时间复杂度O(log n)。

　　性质：

　　1. 每个节点非红即黑

　　2. 根节点是黑的;

　　3. 每个叶节点（叶节点即树尾端NULL指针或NULL节点）都是黑的;

　　4. 如果一个节点是红色的，则它的子节点必须是黑色的。

　　5. 对于任意节点而言，其到叶子节点树NULL指针的每条路径都包含相同数目的黑节点;

　　

 

 

　　B+树

　　维基百科上所定义的方式，即关键字个数比孩子结点个数小1，这种方式是和B树基本等价的。下图就是一颗阶数为4的B+树。

　　

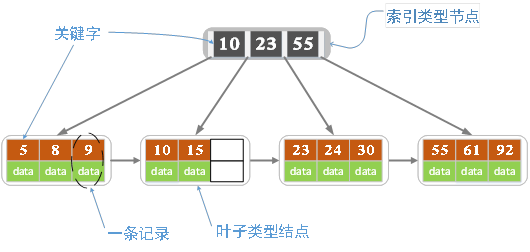
　　1）B+树包含2种类型的结点：内部结点（也称索引结点）和叶子结点。根结点本身即可以是内部结点，也可以是叶子结点。根结点的关键字个数最少可以只有1个。

　　2）B+树与B树最大的不同是内部结点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子结点中。

　　3） m阶B+树表示了内部结点最多有m-1个关键字（或者说内部结点最多有m个子树），阶数m同时限制了叶子结点最多存储m-1个记录。

　　4）内部结点中的key都按照从小到大的顺序排列，对于内部结点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。

　　5）每个叶子结点都存有相邻叶子结点的指针（链表双向查询），叶子结点本身依关键字的大小自小而大顺序链接。

 

　　完全二叉树

　　通常使用数组存放，tree[i]， 该节点的左孩子为tree[2i+1]，右孩子为tree[2i+2]。

 

　　遍历

　　前序遍历

void preTrval(TreeNode *T)
{
    stack<TreeNode*> S;
    TreeNode *pNode = T;
    while (pNode != nullptr || !S.empty())
    {
        if (pNode != nullptr)
        {
            cout << pNode->val<<' ';
            S.push(pNode);
            pNode = pNode->left;
        }
        else
        {
            pNode = S.top();
            S.pop();
            pNode = pNode->right;
        }
    }
}

中序遍历

void midTrval(TreeNode *T)
{
    stack<TreeNode*> S;
    TreeNode *pNode = T;
    while (pNode != nullptr || !S.empty())
    {
        if (pNode != nullptr)
        {
            S.push(pNode);
            pNode = pNode->left;
        }
        else
        {
            pNode = S.top();
            S.pop();
            cout << pNode->val << ' ';
            pNode = pNode->right;
        }
    }
}

后序遍历

void postTrval(TreeNode *T)
{
    TreeNode *pNode = T;
    TreeNode *lastvisit = pNode;
    stack<TreeNode*> S;
    while (pNode || !S.empty())
    {
        while (pNode)
        {
            S.push(pNode);
            pNode = pNode->left;
        }
        pNode = S.top();
        if (pNode->right == nullptr || pNode->right == lastvisit)
        {
            cout << pNode->val << ' ';
            S.pop();
            lastvisit = pNode;
            pNode = nullptr;//输出后获取栈顶
        }
        else
        {
            pNode = pNode->right;
        }
    }
}

按层遍历

void levelTrval(TreeNode *T)
{
    queue<TreeNode*> Q;
    TreeNode *pNode = T;
    Q.push(pNode);
    while (!Q.empty())
    {
        TreeNode *p = Q.front();
        Q.pop();
        cout << p->val << ' ';
        if (p->left)
            Q.push(p->left);
        if (p->right)
            Q.push(p->right);
    }
}