自动提取土壤线-基于Python
以前上遥感课写的记录,我把它搬到这里,原先是jupyter格式。
内容更新以原始发布为准:https://www.wsh233.cn/blog/80582840
背景和意义
土壤在可见光波段(R)与近红外波段(NIR)的反射率具有线性关系,在R-NIR通道的二维坐标中,土壤光谱特性的变化表现为一个由近于原点发射的直线,称之为土壤线,可表示为:
ρNIR = αR +b,其中α,b分别为土壤线的斜率和斜距。
土壤的光谱特征受土壤有机质、氧化铁、粗糙度等众多因素的影响,但是对于同一种土壤来说,其反射光谱在红与近红外波段形成了特定的土壤线,它不仅反映土壤的光
学特性,有助于了解土壤和植被的理化性质与生态特征,并且参与植被指数计算,消除观测场土壤背景的
影响,如垂直植被指数、土壤调整植被指数和转换型土壤调整植被指数等均基于土壤线方程的参数进行计算,另外还可用于表征土壤的不同湿度状况,基于土壤线斜率提出的土壤干旱指数可以有效监测土壤水分。
方法简介
常规提取土壤线的方法,是利用地面实测土壤光谱、影像解译及其他方法从遥感影像上识别出裸土像元,进行土壤线参数的计算。常规方法较为复杂,受人为因素影响较多,并且对于中低分辨率的遥感影像来说,裸土的识别难度较大而难以实行,本文将引入统计学中的相关分析-皮尔逊相关系数与一元线性回归模型,自动提取提取土壤线。
皮尔逊相关系数
用于度量两个变量X和Y之间的相關程度(线性相关),其值介于-1与1之间。在自然科学领域中,该系数广泛用于度量两个变量之间的线性相关程度,它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来。
两个变量之间的皮尔逊相关系数定义为两个变量的协方差除以它们标准差的乘积:
相关系数r值介于[-1,1]之间,r > 0,表示正相关,即两要素同向相关;r < 0,表示负相关,即两要素异向相关。r的值越接近于1,表示两要素的关系越密切;越接近于0,表示两要素的关系不密切。
一元线性回归模型
描述两个要素(变量)之间的线性相关关系,假设两个地理要素(变量)x和y,x为自变量,y为因变量。则一元线性回归模型的基本结构形式为:
数据说明
报告实验数据为Landsat 8 OLI_TIRS 卫星数字产品,条带号为 115,30,下载自地理空间数据云,部分信息如下:。
- 数据标识: LE71150302000161EDC00
- 数据范围:麻栗坡县,云南
- 日期: 2000年
已在ENVI中进行辐射校正预处理。
处理分析
处理环境:Jupyter lab
Python版本:Python3.7 64-bit
数据准备与转换
首先使用rasterio库读取遥感影像,提取遥感影像中的灰度值(DN) ,将DN值转为多维数组。影像默认数据类型为无符号16位整形,需要改为32位浮点型。
# 导入依赖库 import rasterio import numpy as np import pandas as pd import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = "SimHei" # 设置中文字体 mpl.rcParams['agg.path.chunksize'] = 100000000 # 设置散点图最大点数为1亿个 from scipy.optimize import leastsq
# 读取遥感影像,B4.TIF对应红外波段,B5.TIF对应近红外波段 with rasterio.open("./raster/mlp/nir.tif", 'r') as nir_src: nir = nir_src.read(1) with rasterio.open("./raster/mlp/red.tif", 'r') as red_src: red = red_src.read(1)
fig, axs = plt.subplots(1,2, figsize=(20, 10)) axs[0].imshow(red,cmap = plt.get_cmap("gray")) axs[0].set_title("红色波段", fontsize=20, pad=10) axs[1].imshow(nir, cmap = plt.get_cmap("gray")) axs[1].set_title("近红外波段", fontsize=20, pad=10) plt.savefig('./figure/diff.jpeg', dpi=200) plt.show() # 预览遥感影像

将数据转换为一维数组
# 原始波段维度 red nir
array([[65535, 65535, 65535, ..., 65535, 65535, 65535], [65535, 65535, 65535, ..., 65535, 65535, 65535], [65535, 65535, 65535, ..., 65535, 65535, 65535], ..., [65535, 65535, 65535, ..., 65535, 65535, 65535], [65535, 65535, 65535, ..., 65535, 65535, 65535], [65535, 65535, 65535, ..., 65535, 65535, 65535]], dtype=uint16)
max_value = red.max() red = red.astype(np.float32).flatten() / max_value nir = nir.astype(np.float32).flatten() / max_value img_df = pd.DataFrame( {"red":red, "nir":nir}, index=np.arange(len(red)) ) img_df
| red | nir | |
|---|---|---|
| 0 | 1.0 | 1.0 |
| 1 | 1.0 | 1.0 |
| 2 | 1.0 | 1.0 |
| 3 | 1.0 | 1.0 |
| 4 | 1.0 | 1.0 |
| ... | ... | ... |
| 7111659 | 1.0 | 1.0 |
| 7111660 | 1.0 | 1.0 |
| 7111661 | 1.0 | 1.0 |
| 7111662 | 1.0 | 1.0 |
| 7111663 | 1.0 | 1.0 |
7111664 rows × 2 columns
筛选数据
-
获取初始土壤点——横坐标所对应的纵坐标值最小的点。
-
统计特征空间中,横轴的最大/小值,设置组距,将所有像元点按照横轴波段反射率归入不同组,接着提取每组中纵轴波段反射率最小的像元点和其横轴区间均值,构成(xi,yi)土壤点集。
-
自适应区间选取,由于初始化土壤点集并非全部都是土壤点,需要对其作进一步筛选。我将初始土壤点集划分为0%50%,0%75%,0%100,25%75%,25%~100%五个子集。然后逐个计算子集的最小二乘相关系数,最大者即确认为有效点集。
fig, ax = plt.subplots(1,1, figsize=(10, 10)) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) ax.set_ylabel("NIR 反射率", fontsize=15) ax.set_xlabel("RED 反射率", fontsize=15) ax.plot(img_df.red, img_df.nir, '.') plt.show()
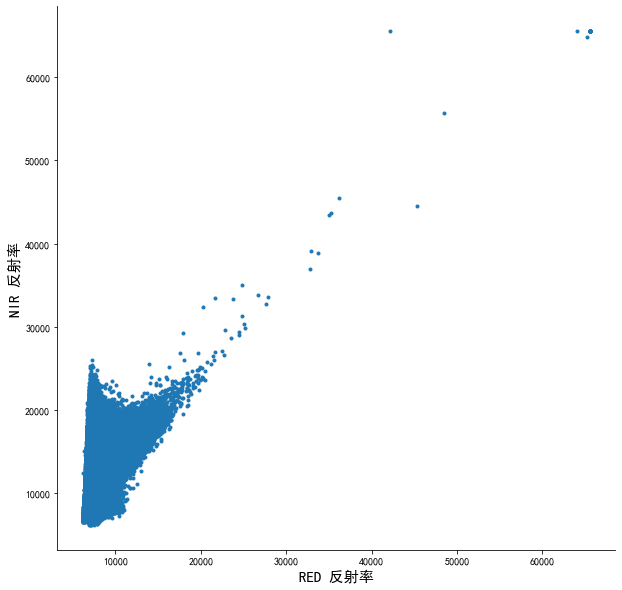
catos = pd.cut(img_df.red, bins=256, right=True, precision=5, labels=np.arange(256)) img_df['class'] = catos # 将分类结果添加到面板数据内 img_df
| red | nir | class | |
|---|---|---|---|
| 0 | 1.0 | 1.0 | 255 |
| 1 | 1.0 | 1.0 | 255 |
| 2 | 1.0 | 1.0 | 255 |
| 3 | 1.0 | 1.0 | 255 |
| 4 | 1.0 | 1.0 | 255 |
| ... | ... | ... | ... |
| 7111659 | 1.0 | 1.0 | 255 |
| 7111660 | 1.0 | 1.0 | 255 |
| 7111661 | 1.0 | 1.0 | 255 |
| 7111662 | 1.0 | 1.0 | 255 |
| 7111663 | 1.0 | 1.0 | 255 |
7111664 rows × 3 columns
gb = img_df.groupby(by="class") nir_min = gb['nir'].min().fillna(0) red_mean = gb['red'].mean().fillna(0) r_df = pd.DataFrame({"red": red_mean, "nir": nir_min}) r_df
| red | nir | |
|---|---|---|
| class | ||
| 0 | 0.096422 | 0.099825 |
| 1 | 0.099828 | 0.100496 |
| 2 | 0.103013 | 0.103349 |
| 3 | 0.106333 | 0.094331 |
| 4 | 0.109638 | 0.094682 |
| ... | ... | ... |
| 251 | 0.000000 | 0.000000 |
| 252 | 0.000000 | 0.000000 |
| 253 | 0.000000 | 0.000000 |
| 254 | 0.994461 | 0.989120 |
| 255 | 1.000000 | 1.000000 |
256 rows × 2 columns
cut方法用于将数据分段,这里设定分为256组,
然后获取每组内红色波段(red)的平均值和近红外波段(nir)的最小值。
这样子便获得了土壤点集,分别是近红外最小值——nir_min和红色平均值——red_mean,构建土壤点集面板数据
现在编写计算相关系数代码,分别计算0%50%,0%75%,0%100,25%75%,25%~100%这五个子集的相关系数
import math # 计算相关系数函数 def r_calcu(a, b): x = a.to_list() y = b.to_list() sum_ref = 0 x_sum = 0 y_sum = 0 x_mean = sum(x) / len(x) y_mean = sum(y) / len(y) for i in range(len(x)): sum_ref += (x[i] - x_mean) * (y[i] - y_mean) x_sum += math.pow((x[i] - x_mean), 2) y_sum += math.pow((y[i] - y_mean), 2) res = sum_ref / (math.sqrt((x_sum) * y_sum)) print("R values: %.10f" % res) return res
box = [(0, 128), (0, 192), (0, 256), (64, 192), (64, 256)] for b in box: data = r_df.iloc[b[0]: b[1]] r_calcu(data.red, data.nir)
R values: 0.9896115364 R values: 0.9882301318 R values: 0.9887827549 R values: 0.9930419777 R values: 0.9908521183
结果五个子集中相关性最大为子集25%-75%,确认为有效土壤集。
得到有效土壤集,接下来借助scikit库对回归线作拟合。
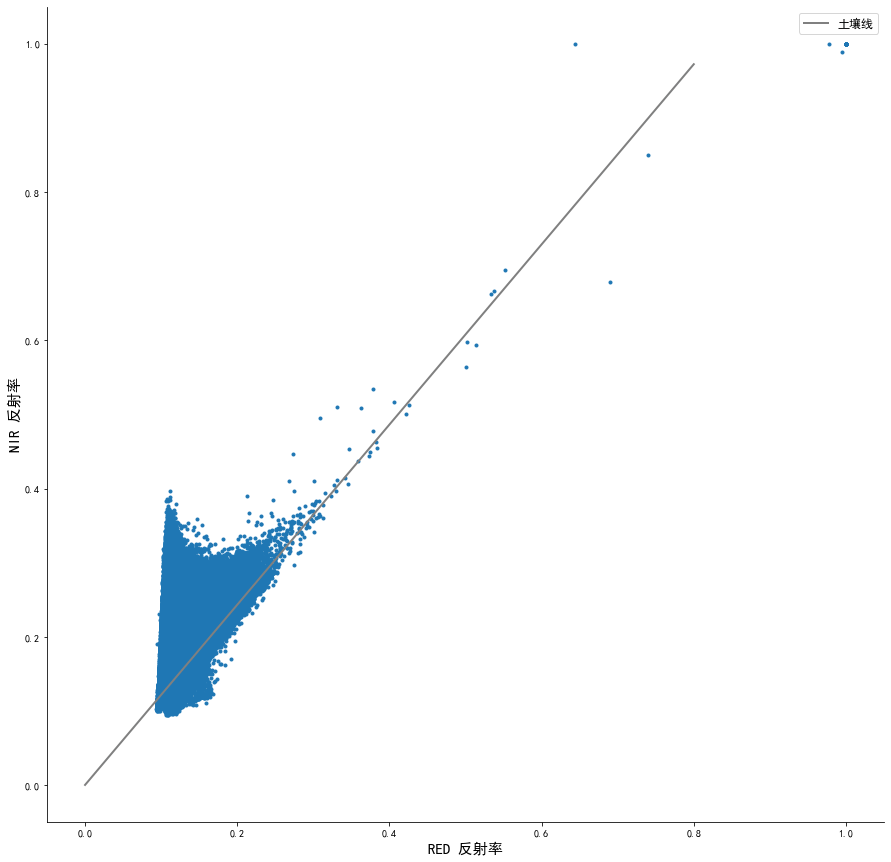
# 拟合残差函数 def err(p, x, y): return p[0] * x + p[1] -y #参数p 为最小二乘法拟合的初值 #我试了多个参数,结果是一致的 p = [0.7, 0.8] ret = leastsq(err, p, args=(r_df.red[64: 192], r_df.nir[64: 192]))#返回参数为一个包含拟合后参数的元组 k,b = ret[0] plt.figure(figsize=(15, 15)) x = np.linspace(0,0.8, 20) y = x * k + b # 绘制图像 fig, ax = plt.subplots(1,1, figsize=(15, 15)) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) ax.set_ylabel("NIR 反射率", fontsize=15) ax.set_xlabel("RED 反射率", fontsize=15) #ax.set_title("土壤线", fontsize=20, pad=10) ax.plot(img_df.red, img_df.nir, '.') ax.plot(x, y, linewidth=2, color="gray", label="土壤线") plt.legend(fontsize=12, loc="upper right") #plt.savefig("./figure/solil_raw.jpeg", dpi=200) plt.show()




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 推荐几款开源且免费的 .NET MAUI 组件库
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· Trae初体验