摘要： 
泰勒公式的理解和快速推导，格雷戈里-牛顿插值公式的简单推导。其实，泰勒公式本质就是用多项幂级数逼近一个单变量函数，也可以说是使任何单变量函数都可以展开成幂级数。假设我们在取点时，特意使任意相邻两点之间的水平间距都相等。佩亚诺型余项和拉格朗日余项。泰勒级数和泰勒展开式，根据上述推导，实际上当我们已知无数个点，即时，泰勒公式具有无穷项，它就像幂级数,称之为泰勒级数。但是在得到公式的过程中，我们却没有去讨论级数的是否收敛。泰勒展开式是特殊的泰勒级数，或者说是收敛情况下的泰勒级数，其具有收敛区间，在收敛区间内，和一定存在。麦克劳林公式 阅读全文
泰勒公式的理解和快速推导，格雷戈里-牛顿插值公式的简单推导。其实，泰勒公式本质就是用多项幂级数逼近一个单变量函数，也可以说是使任何单变量函数都可以展开成幂级数。假设我们在取点时，特意使任意相邻两点之间的水平间距都相等。佩亚诺型余项和拉格朗日余项。泰勒级数和泰勒展开式，根据上述推导，实际上当我们已知无数个点，即时，泰勒公式具有无穷项，它就像幂级数,称之为泰勒级数。但是在得到公式的过程中，我们却没有去讨论级数的是否收敛。泰勒展开式是特殊的泰勒级数，或者说是收敛情况下的泰勒级数，其具有收敛区间，在收敛区间内，和一定存在。麦克劳林公式 阅读全文
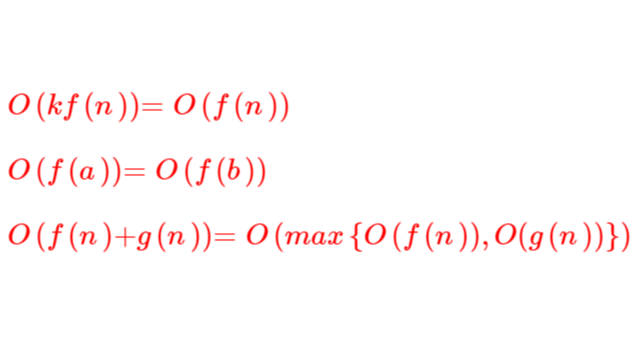时间复杂度的理解和计算，研究一个算法，我们先给出条件——忽略硬件的影响、忽略待处理数据的具体值，那么显而易得的，不同的单条语句执行时间相同，记为单位时间t。此时，算法执行时间T与所有语句执行次数$f$有关，而所有语句执行次数$f$又与待处理数据规模n有关，因此，T与n有关。我们在测算某个算法的时间效率时，无法做到将每个算法都运行一次。因此，我们通常采用“纸上谈兵”的方法，即在纸面上利用分析估算来研究一个算法的时间效率。“纸上谈兵”要谈什么兵？对，比较不同算法的T(n)的大小，怎么比？对！比值！！在实际生活中，我们通常研究的是${n \to \infty }$时的值的大小，哦~，求极限。用O来表示增长趋势。求时间复杂度时只需要求执行次数最多的语句的执行次数即可 
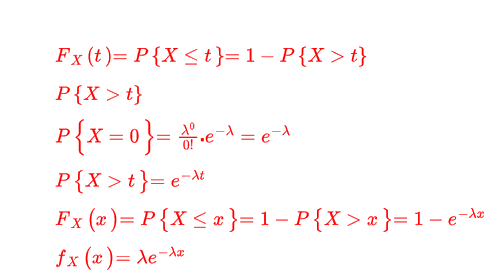指数分布的分布函数和概率密度函数的推导，牢记指数分布的分布函数为1-e^(-λx)，很多人在初学时，只记得指数分布的概率密度函数，e^(-λx)，再利用积分计算概率，这是对的，但有人利用积分直接得分布函数，这样就错了。从上述过程来看，指数分布公式里的λ与单位时间下泊松分布的λ相同，不是单位时间下就不同了。以下举例： 
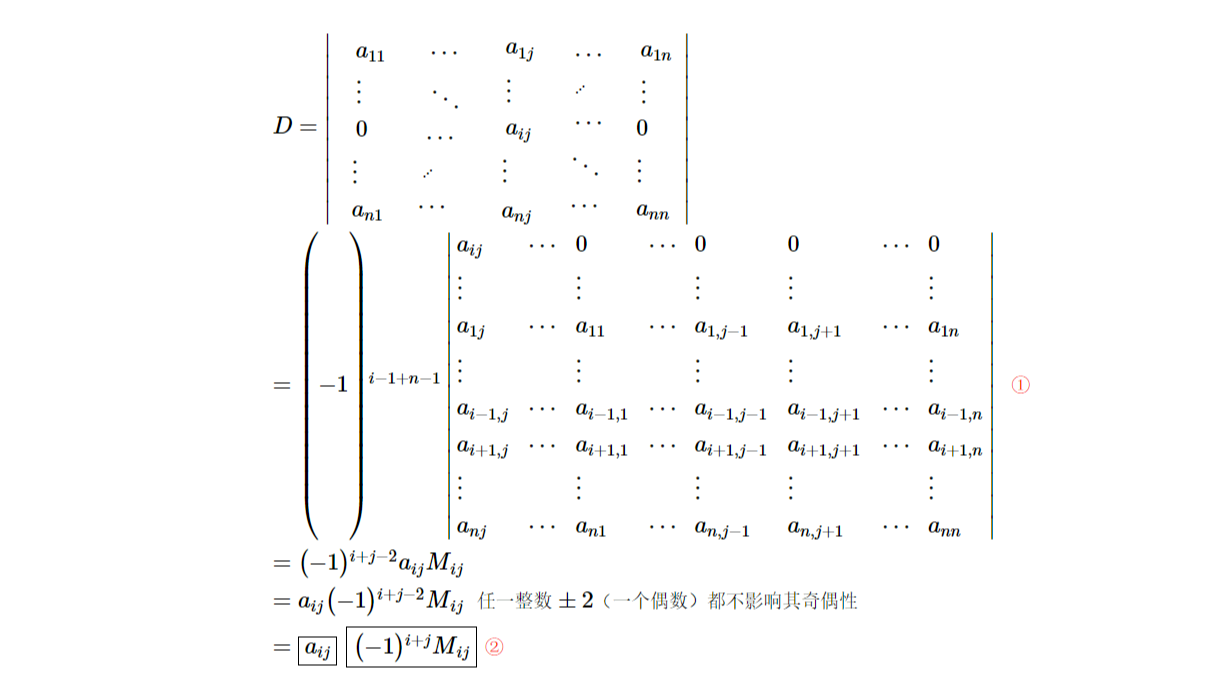代数余子式的由来/代数余子式为什么-1的系数是ⁱ⁺ʲ?/证明一个n阶行列式，如果其中第i行（或第j列）所有元素除aᵢⱼ外都为零，那么这行列式等于aᵢⱼ与它的代数余子式的乘积/证明行列式按行（列）展开法则：n（n>1）阶行列式等于它任意一行（列）的所有元素与它们对应的代数余子式的乘积的和。 
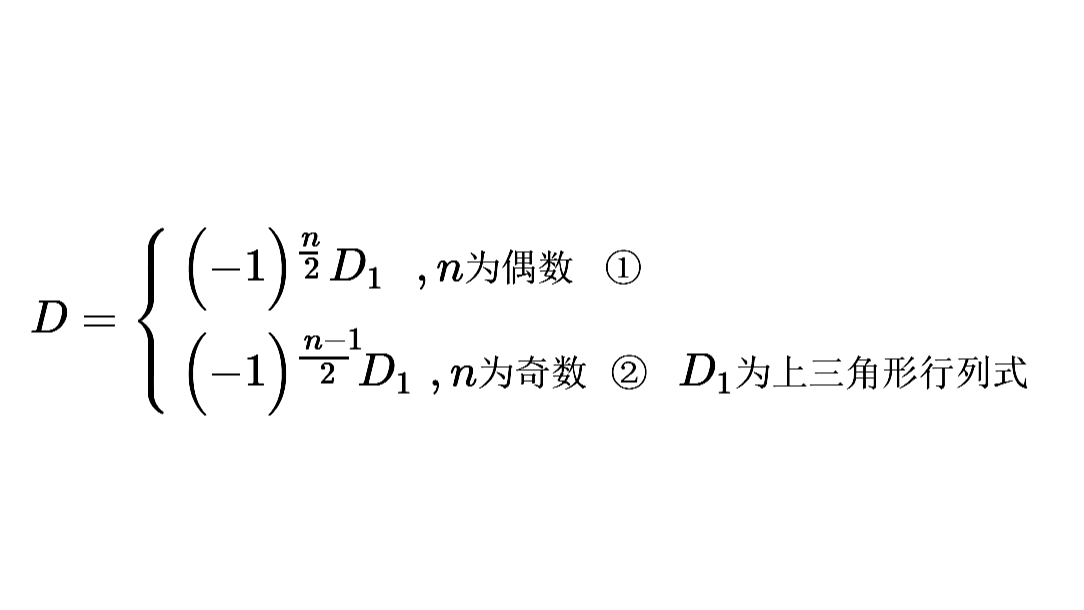副三角形行列式转成上（下）三角形行列式为什么依次对换而不用第n行直接对换首行，第n-1行直接对换次行
1.简而言之，可以用第n行直接对换首行，第n-1行直接对换次行，直到行列式完全上下翻转。
但需要对n讨论奇偶。
2.转换过程既然是上下翻转，那就应该是乘以一个行列式上下翻转系数：将第n行反复进行相邻对换到首行需要n-1次，再将之后的行列式第n行反复进行相邻对换到次行需要n-2次，因此副三角形行列式反转成上（下）三角形行列式需要n(n-1)/2次（每次仅允许相邻对换）。 
样本方差S²中为什么是乘以1/(n-1)或者说除以n-1?贝塞尔校正，无偏估计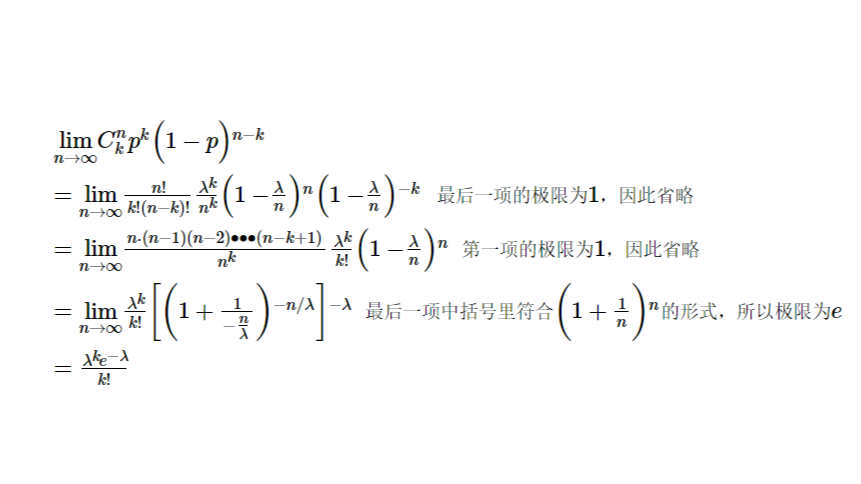 
泊松分布概率公式的推导 
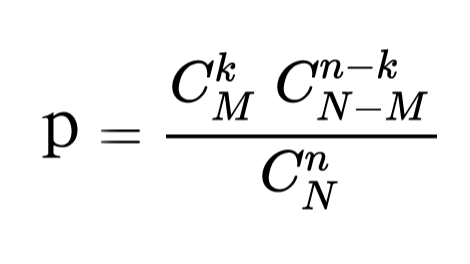怎么理解超几何分布概率公式：p=C(M,k)C(N-M,n-k)/C(N,n) 
实现分页数据请求的思路/Element UI(Plus)的分页模板（Vue3.x写法），（直接使用script引入vue.js）
实现分页数据请求的思路：分页面对的场景是大量的数据导致渲染速度慢，甚至出现卡顿、掉帧。因此引入分页组件后，我们需要考虑如何将数据与分页相结合。
思路一：前端在请求数据时不请求全部的数据，而是带上分页大小、页码等限定条件。
优点：每一次请求的数据量小，初次渲染速度更快。缺点：每次执行切换页面等操作都会请求数据，对服务器端要求高。
思路二：前端在请求数据时请求全部的数据，服务器端将数据整理成JSON或其他格式，便于前端根据索引分块使用。
优点：不需要反复请求数据，每次执行切换页面等操作渲染速度更快。缺点：初次请求数据量大，遇到异常巨大的数据量时，初次渲染速度慢。
我的想法是在数据量不是异常大的情况下选思路一，数据量异常大的情况下两种思路结合，在不明显影响数据渲染速度的前提下，每次请求数据都尽可能的大。 
HTML+CSS+JS制作一个黑灰色简约时钟，这次借鉴了网络上的代码，利用JS动态创建元素，减少html语句的数量，也便于与vue、react等语言进行结合。