戈小戈

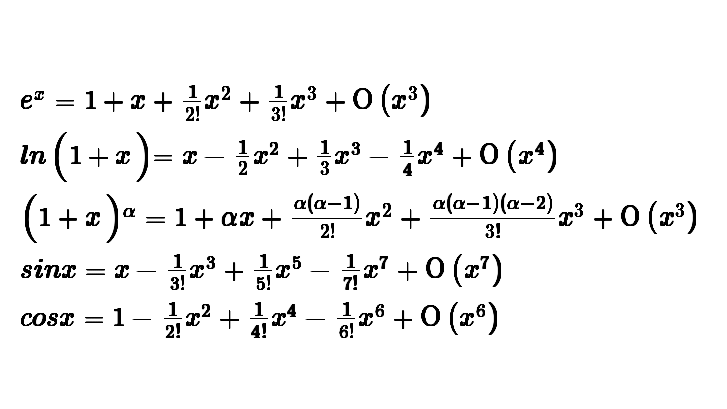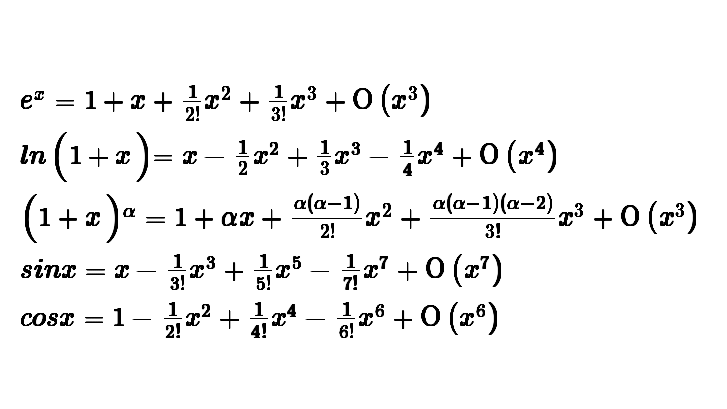摘要： 当我们不知道泰勒公式或者麦克劳林公式具体内容时：泰勒公式本质就是用多项幂级数逼近一个单变量函数，也可以说是使任何单变量函数都可以展开成幂级数。当我们不知道泰勒公式或者麦克劳林公式具体内容时：常用的泰勒公式的快速推导,1.步骤：(1).公式写出来,(2).算出，直接往公式里填。最后可以加个余项，选佩亚诺余项即可。 阅读全文

摘要： 泰勒公式的理解和快速推导，格雷戈里-牛顿插值公式的简单推导。其实，泰勒公式本质就是用多项幂级数逼近一个单变量函数，也可以说是使任何单变量函数都可以展开成幂级数。假设我们在取点时，特意使任意相邻两点之间的水平间距都相等。佩亚诺型余项和拉格朗日余项。泰勒级数和泰勒展开式，根据上述推导，实际上当我们已知无数个点，即时，泰勒公式具有无穷项，它就像幂级数,称之为泰勒级数。但是在得到公式的过程中，我们却没有去讨论级数的是否收敛。泰勒展开式是特殊的泰勒级数，或者说是收敛情况下的泰勒级数，其具有收敛区间，在收敛区间内，和一定存在。麦克劳林公式 阅读全文