常用的泰勒公式的快速推导
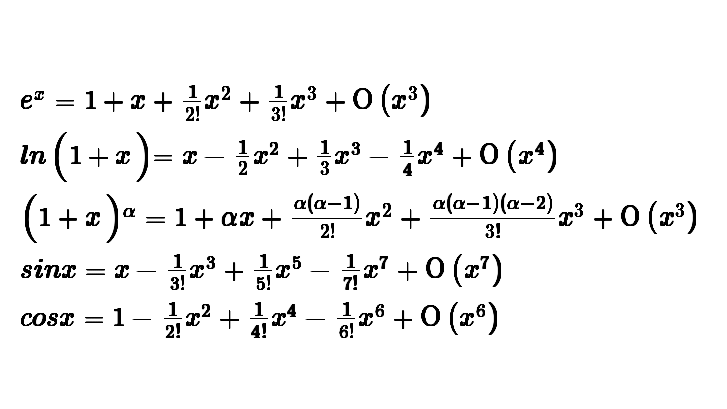
当我们不知道泰勒公式或者麦克劳林公式具体内容时：泰勒公式本质就是用多项幂级数逼近一个单变量函数，也可以说是使任何单变量函数都可以展开成幂级数。当我们不知道泰勒公式或者麦克劳林公式具体内容时：常用的泰勒公式的快速推导,1.步骤：(1).公式写出来,(2).算出，直接往公式里填。最后可以加个余项，选佩亚诺余项即可。
常用函数的泰勒公式的快速推导
前言：重在记录，可能出错。
· 当我们不知道泰勒公式或者麦克劳林公式具体内容时：
一、基本原理：
泰勒公式本质就是用多项幂级数逼近一个单变量函数，也可以说是使任何单变量函数都可以展开成幂级数。
这句话用公式表达出来就是：
\[{f \left( x \left) =a\mathop{{}}\nolimits_{{0}}+a\mathop{{}}\nolimits_{{1}}x+a\mathop{{}}\nolimits_{{2}}x\mathop{{}}\nolimits^{{2}}+a\mathop{{}}\nolimits_{{3}}x\mathop{{}}\nolimits^{{3}}+ \cdots +a\mathop{{}}\nolimits_{{n}}x\mathop{{}}\nolimits^{{n}}\right. \right. }
\]
其中\(a\mathop{{}}\nolimits_{{i}}\)均为常数，怎么求呢？对此式求导，令x=0。
二、常用函数的泰勒公式的快速推导：
例：求ln(1+x)的泰勒公式：
\[{\begin{array}{*{20}{l}}{1.\text{ }\text{ }\text{ }ln \left( 1+x \left) =a\mathop{{}}\nolimits_{{0}}+a\mathop{{}}\nolimits_{{1}}x+a\mathop{{}}\nolimits_{{2}}x\mathop{{}}\nolimits^{{2}}+a\mathop{{}}\nolimits_{{3}}x\mathop{{}}\nolimits^{{3}}+ \cdots \right. \right. }\\{\text{当}x=0\text{时}\text{，}a\mathop{{}}\nolimits_{{0}}=ln1=0\text{，}\text{对}1\text{式}\text{求}\text{导}，\text{得}\text{到}2\text{式}}\\{}\\{2.\text{ }\text{ } \left( -1 \left) \mathop{{}}\nolimits^{{0}}\frac{{1}}{{1+x}}=a\mathop{{}}\nolimits_{{1}}+2a\mathop{{}}\nolimits_{{2}}x+3a\mathop{{}}\nolimits_{{3}}x\mathop{{}}\nolimits^{{2}}+ \cdots \right. \right. }\\{\text{当}x=0\text{时}\text{，}a\mathop{{}}\nolimits_{{1}}=1\text{，}\text{对}2\text{式}\text{求}\text{导}，\text{得}\text{到}3\text{式}}\\{}\\{3.\text{ }\text{ } \left( -1 \left) \mathop{{}}\nolimits^{{1}}\frac{{1}}{{ \left( 1+x \left) \mathop{{}}\nolimits^{{2}}\right. \right. }}=2a\mathop{{}}\nolimits_{{2}}+3*2a\mathop{{}}\nolimits_{{3}}x+ \cdots \right. \right. }\\{\text{当}x=0\text{时}，a\mathop{{}}\nolimits_{{2}}=-\frac{{1}}{{2}}\text{，}\text{对}3\text{式}\text{求}\text{导}，\text{得}\text{到}4\text{式}}\\{}\\{4.\text{ }\text{ } \left( -1 \left) \mathop{{}}\nolimits^{{2}}*2*\frac{{1}}{{ \left( 1+x \left) \mathop{{}}\nolimits^{{3}}\right. \right. }}=3*2a\mathop{{}}\nolimits_{{3}}+ \cdots \text{ }\right. \right. }\\{\text{当}x=0\text{时}，a\mathop{{}}\nolimits_{{3}}=\frac{{1}}{{3}}}\end{array}}
\]
综上，\({ln \left( 1+x \left) =x-\frac{{1}}{{2}}x\mathop{{}}\nolimits^{{2}}+\frac{{1}}{{3}}x\mathop{{}}\nolimits^{{3}}+O \left( x\mathop{{}}\nolimits^{{4}} \right) \right. \right. }\)
· 当我们知道泰勒公式或者麦克劳林公式具体内容时：
一、基本原理：
在我的泰勒公式的理解和简单推导，格雷戈里-牛顿插值公式的简单推导博客里，我们得到了泰勒公式：
\[\color{red}{\begin{array}{*{20}{l}}{{f \left( x \left) =f \left( x\mathop{{}}\nolimits_{{0}} \right) +{f \prime } \left( x\mathop{{}}\nolimits_{{0}} \left) \left( x-x\mathop{{}}\nolimits_{{0}} \left) +\frac{{{f''} \left( x\mathop{{}}\nolimits_{{0}} \right) }}{{2!}} \left( x-x\mathop{{}}\nolimits_{{0}} \left) \mathop{{}}\nolimits^{{2}}+ \cdots +\frac{{f\mathop{{}}\nolimits^{{ \left( n \right) }} \left( x\mathop{{}}\nolimits_{{0}} \right) }}{{n!}} \left( x-x\mathop{{}}\nolimits_{{0}} \left) \mathop{{}}\nolimits^{{n}}+R\mathop{{}}\nolimits_{{n+1}} \left( x \left) \right. \right. \right. \right. \right. \right. \right. \right. \right. \right. \right. \right. }}\\{R\mathop{{}}\nolimits_{{n+1}} \left( x \left) \text{是}\text{余}\text{项}\right. \right. }\end{array}}
\]
当\({x\mathop{{}}\nolimits_{{0}}=0}\)时，我们得到了，麦克劳林公式：
\[\color{red}{{f \left( x \left) =f \left( 0 \right) +{f \prime } \left( 0 \left) x+\frac{{{f''} \left( 0 \right) }}{{2!}}x\mathop{{}}\nolimits^{{2}}+ \cdots +\frac{{f\mathop{{}}\nolimits^{{ \left( n \right) }} \left( 0 \right) }}{{n!}}x\mathop{{}}\nolimits^{{n}}+R\mathop{{}}\nolimits_{{n+1}} \left( x \left) \right. \right. \right. \right. \right. \right. }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }R\mathop{{}}\nolimits_{{n+1}} \left( x \left) \text{是}\text{余}\text{项}\right. \right. }
\]
想要快速求出常用函数的泰勒公式，只需要求常用函数的不同阶导即可。
二、常用函数的泰勒公式的快速推导：
1.步骤：(1).公式写出来
\[\color{red}{{f \left( x \left) =f \left( 0 \right) +{f \prime } \left( 0 \left) x+\frac{{{f''} \left( 0 \right) }}{{2!}}x\mathop{{}}\nolimits^{{2}}+ \cdots +\frac{{f\mathop{{}}\nolimits^{{ \left( n \right) }} \left( 0 \right) }}{{n!}}x\mathop{{}}\nolimits^{{n}}+R\mathop{{}}\nolimits_{{n+1}} \left( x \left) \right. \right. \right. \right. \right. \right. }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }R\mathop{{}}\nolimits_{{n+1}} \left( x \left) \text{是}\text{余}\text{项}\right. \right. }
\]
(2).算出$ {{f \left( 0 \left) \text{、}{f \prime } \left( 0 \left) \text{、}{{f''} \left( 0 \right) }\text{、} \cdots \text{、}f\mathop{{}}\nolimits^{{ \left( n \right) }} \left( 0 \left) \right. \right. \right. \right. \right. \right. }}$，直接往公式里填。最后可以加个余项，选佩亚诺余项即可。
(3).例子：
\[{\begin{array}{*{20}{l}}{e\mathop{{}}\nolimits^{{x}}=1+x+\frac{{1}}{{2!}}x\mathop{{}}\nolimits^{{2}}+\frac{{1}}{{3!}}x\mathop{{}}\nolimits^{{3}}+ {\rm O} \left( x\mathop{{}}\nolimits^{{3}} \right) }\\{ln \left( 1+x \left) =x-\frac{{1}}{{2}}x\mathop{{}}\nolimits^{{2}}+\frac{{1}}{{3}}x\mathop{{}}\nolimits^{{3}}-\frac{{1}}{{4}}x\mathop{{}}\nolimits^{{4}}+ {\rm O} \left( x\mathop{{}}\nolimits^{{4}} \right) \right. \right. }\\{ \left( 1+x \left) \mathop{{}}\nolimits^{{ \alpha }}=1+ \alpha x+\frac{{ \alpha \left( \alpha -1 \right) }}{{2!}}x\mathop{{}}\nolimits^{{2}}+\frac{{ \alpha \left( \alpha -1 \left) \left( \alpha -2 \right) \right. \right. }}{{3!}}x\mathop{{}}\nolimits^{{3}}+ {\rm O} \left( x\mathop{{}}\nolimits^{{3}} \right) \right. \right. }\\{sinx=x-\frac{{1}}{{3!}}x\mathop{{}}\nolimits^{{3}}+\frac{{1}}{{5!}}x\mathop{{}}\nolimits^{{5}}-\frac{{1}}{{7!}}x\mathop{{}}\nolimits^{{7}}+ {\rm O} \left( x\mathop{{}}\nolimits^{{7}} \right) }\\{cosx=1-\frac{{1}}{{2!}}x\mathop{{}}\nolimits^{{2}}+\frac{{1}}{{4!}}x\mathop{{}}\nolimits^{{4}}-\frac{{1}}{{6!}}x\mathop{{}}\nolimits^{{6}}+ {\rm O} \left( x\mathop{{}}\nolimits^{{6}} \right) }\end{array}}
\]
