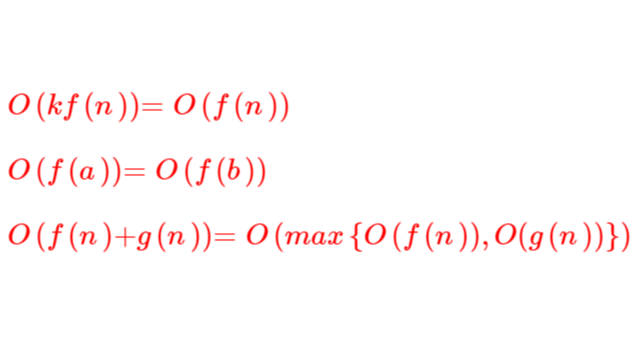
时间复杂度的理解和计算,研究一个算法,我们先给出条件——忽略硬件的影响、忽略待处理数据的具体值,那么显而易得的,不同的单条语句执行时间相同,记为单位时间t。此时,算法执行时间T与所有语句执行次数
f有关,而所有语句执行次数
f又与待处理数据规模n有关,因此,T与n有关。我们在测算某个算法的时间效率时,无法做到将每个算法都运行一次。因此,我们通常采用“纸上谈兵”的方法,即在纸面上利用分析估算来研究一个算法的时间效率。“纸上谈兵”要谈什么兵?对,比较不同算法的T(n)的大小,怎么比?对!比值!!在实际生活中,我们通常研究的是
n→∞时的值的大小,哦~,求极限。用O来表示增长趋势。求时间复杂度时只需要求执行次数最多的语句的执行次数即可
时间复杂度的理解和计算
前言:重在记录,可能出错。
一、算法执行时间的表示
研究一个算法,我们先给出条件——忽略硬件的影响、忽略待处理数据的具体值,那么显而易得的,不同的单条语句执行时间相同,记为单位时间t。此时,算法执行时间T与所有语句执行次数f有关,而所有语句执行次数f又与待处理数据规模n有关,因此,T与n有关。

我们用函数f(n)、T(n)分别表示所有语句执行次数f和算法执行时间T和待处理数据规模n之间的关系。即:
T(n)=f(n)∙t
二、时间复杂度的理解
1. 时间复杂度是用来大约表示算法执行时间随着待处理数据规模增大的增长趋势。
2. 我们在测算某个算法的时间效率时,无法做到将每个算法都运行一次。因此,我们通常采用“纸上谈兵”的方法,即在纸面上利用分析估算来研究一个算法的时间效率。
3. “纸上谈兵”要谈什么兵?对,比较不同算法的T(n)的大小,怎么比?对!比值!!在实际生活中,我们通常研究的是n→∞时的值的大小,哦~,求极限。
limn→∞T1(n)T2(n)=limn→∞f1(n)tf2(n)t=limn→∞f1(n)f2(n) ? 1
分析这个式子,我们发现在n趋近于∞的过程中,当T1(n)的增长快于T2(n)时,必然存在一个n0∈R+,满足n>n0,T1(n)>T2(n)。对于单调递增函数,反过来依然成立,也就是说:limn→∞T(n)越大,T(n)增长越快。
我们用时间复杂度来表示函数的增长趋势,用大O符号来表示函数无穷大渐近的值(在这里可以理解为一个单调递增函数的最大值),则O越大,时间复杂度越大。常见增长趋势大小的有O(常数)<O(对数函数)<O(幂函数)<O(指数函数)。具体的有:
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)
为了便于分析,我们直接说时间复杂度等于O(f(n)),也就是用O来表示增长趋势。
三、时间复杂度的计算
O(f(n))来表示增长趋势,显而易得的,有以下结论:
1. 趋势乘以一个常数k,趋势不变。
2. 待处理数据的规模n不影响趋势的大小
3. 大趋势加上一个小趋势仍等于自身大趋势不变。
用公式表示以上两个结论,我们就可以得到时间复杂度的计算公式:
1. O(kf(n))=O(f(n))
2. O(f(a))=O(f(b))
3. O(f(n)+g(n))=O(max{O(f(n)),O(g(n))})
例:有以下程序片段,求时间复杂度:
1.
| void fun(int n){ |
| int a; |
| for(int i=0;i<6;i++){ |
| a=i; |
| } |
| } |
所有语句执行次数f(n)=1+1+7+6+6=21,时间复杂度为:
O(f(n))=O(21)=O(21*1)=O(1)=O(6*1)=O(6)
2.
| void fun(int n){ |
| int a; |
| for(int i=0;i<n;i++){ |
| a=i; |
| } |
| } |
所有语句执行次数f(n)=1+1+(n+1)+n+n=3n+3,时间复杂度为:
O(f(n))=O(3n+3)=O(max{O(3n),O(3)})=O(3n)=O(n)
3.
| void fun(int n){ |
| int a; |
| for(int i=0;i<n;i++){ |
| for(int j=0;j<n;j++){ |
| a=j; |
| } |
| } |
| } |
所有语句执行次数f(n)=1+1+(n+1)+n+n+(n²+n)+n²+n²=3n²+4n+3,时间复杂度为:
O(f(n))=O(3n²+4n+3)=O(max{O(3n²),O(4n),O(3)})=O(3n²)=O(n²)
综上,可以看出求时间复杂度时只需要求执行次数最多的语句的执行次数,一个含n的项式,并且将系数定为1即可,执行次数最多的语句一般就是最深层的语句(最基本语句)。
4.
| void fun(int n){ |
| int a; |
| for(int i=1;i<n;i*=2){ |
| a=i; |
| |
| |
| |
| |
| |
| } |
| } |
| } |
所有语句执行次数log₂(n-Δ(n)),0≤Δ(n)≤n-1,代表误差,时间复杂度为:
O(log₂(n-Δ(n)))=O(log₂n)=O(logn)
注:实际上根据换底公式,
O(log2n)=O(log3nlog32)=O(1log32∙log3n)=O(log3n),1log32是个常数
同理可得,所有logₓn样式的对数函数的趋势都相同。所以可以简写为logn

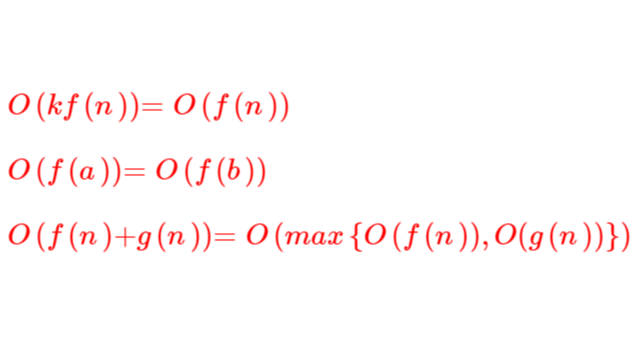 时间复杂度的理解和计算,研究一个算法,我们先给出条件——忽略硬件的影响、忽略待处理数据的具体值,那么显而易得的,不同的单条语句执行时间相同,记为单位时间t。此时,算法执行时间T与所有语句执行次数
时间复杂度的理解和计算,研究一个算法,我们先给出条件——忽略硬件的影响、忽略待处理数据的具体值,那么显而易得的,不同的单条语句执行时间相同,记为单位时间t。此时,算法执行时间T与所有语句执行次数


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 通过 API 将Deepseek响应流式内容输出到前端
· 因为Apifox不支持离线,我果断选择了Apipost!