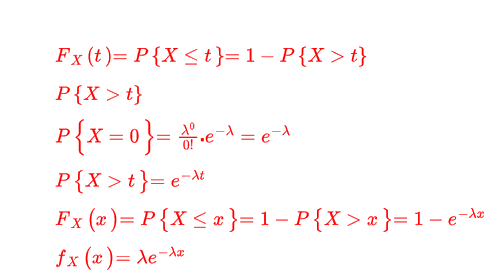
指数分布的分布函数和概率密度函数的推导，牢记指数分布的分布函数为1-e^(-λx)
指数分布的分布函数和概率密度函数的推导，牢记指数分布的分布函数为1-e^(-λx)，很多人在初学时，只记得指数分布的概率密度函数，e^(-λx)，再利用积分计算概率，这是对的，但有人利用积分直接得分布函数，这样就错了。从上述过程来看，指数分布公式里的λ与单位时间下泊松分布的λ相同，不是单位时间下就不同了。以下举例：
指数分布的分布函数和概率密度函数的推导，牢记指数分布的分布函数为1-e^(-λx)
前言：重在记录，可能出错。
之前推导出了泊松分布的概率公式——泊松分布概率公式的推导，现在推导一下指数分布的分布函数和概率密度函数。
很多人在初学时，只记得指数分布的概率密度函数，e^(-λx)，再利用积分计算概率，这是对的，但有人利用积分直接得分布函数，这样就错了。
1. 首先，指数分布描述的是等待事件下一次发生的时间间隔t的概率，分布函数为:
\[\color{red}{F\mathop{{}}\nolimits_{{X}} \left( t \left) =P \left\{ X \le t \left\} =1-P \left\{ X > t \right\} \right. \right. \right. \right. }
\]
求分布函数可以先求\(\color{red}{P \left\{ X > t \right\} }\)
2. 其次，\(\color{red}{P \left\{ X > t \right\} }\)描述的是等待事件下一次发生的时间间隔大于t的概率，换一种说法，即在t时间（t个单位时间）内事件未发生（发生次数为0）的概率。描述一个事件在一段时间内发生次数的概率，恰好是泊松分布。
3.每个单位时间内事件发生次数为0的概率使用泊松分布转换为代数式为
\[\color{red}{P \left\{ X=0 \left\} =\frac{{ \lambda \mathop{{}}\nolimits^{{0}}}}{{0!}}⸳e\mathop{{}}\nolimits^{{- \lambda }}=e\mathop{{}}\nolimits^{{- \lambda }}\right. \right.}
\]
那么‘在t个单位时间内事件发生次数为0的概率’，即
\[\color{red}{P \left\{ X > t \left\} =e\mathop{{}}\nolimits^{{- \lambda t}}\right. \right.}
\]
4. 最后，综上可得，将t替换为x，当x≥0时，指数分布的分布函数为：
\[\color{red}{F\mathop{{}}\nolimits_{{X}} \left( x \left) =P \left\{ X \le x \left\} =1-P \left\{ X > x \left\} =1-e\mathop{{}}\nolimits^{{- \lambda x}}\right. \right. \right. \right. \right. \right. }
\]
当x≥0时，指数分布的概率密度函数为：
\[\color{red}{f\mathop{{}}\nolimits_{{X}} \left( x \left) = \lambda e\mathop{{}}\nolimits^{{- \lambda x}}\right. \right. }
\]
5. 从上述过程来看，指数分布公式里的λ与单位时间下泊松分布的λ相同，不是单位时间下就不同了。以下举例：
例题：公司茶水间饮水机，平均每分钟有一名员工接水并离开。分别以泊松分布和指数分布计算，三分钟没有员工在茶水间饮水机接水并离开的概率。
解：
(1).泊松分布：
\[\begin{array}{*{20}{l}}{E \left( x \left) =3= \lambda \mathop{{}}\nolimits_{{1}}\text{ }\text{ }\text{ }\text{ }\text{ }\text{问}\text{三}\text{分}\text{钟}\text{，}\text{所}\text{以}\text{此}\text{时}\text{期}\text{望}\text{为}3\right. \right. }\\{P \left( x=0 \left) =\frac{{ \lambda \mathop{{}}\nolimits_{{1}}\mathop{{}}\nolimits^{{0}}}}{{0!}}e\mathop{{}}\nolimits^{{- \lambda \mathop{{}}\nolimits_{{1}}}}=e\mathop{{}}\nolimits^{{-3}}\right. \right. }\end{array}
\]
(2).指数分布：
\[{\begin{array}{*{20}{l}}{E \left( t \left) =1=\frac{{1}}{{ \lambda \mathop{{}}\nolimits_{{2}}}}\text{ }\text{ }\text{ }\text{ }\text{ }\text{指}\text{数}\text{分}\text{布}\text{的}\text{期}\text{望}\text{仍}\text{为}1\right. \right. }\\{ \lambda \mathop{{}}\nolimits_{{2}}=1}\\{P \left( \text{t} > 3 \left) ={\mathop{ \int }\nolimits_{{3}}^{{+ \infty }}{ \lambda \mathop{{}}\nolimits_{{2}}e\mathop{{}}\nolimits^{{- \lambda \mathop{{}}\nolimits_{{2}}t}}dt=e\mathop{{}}\nolimits^{{-3}}}}\right. \right. }\end{array}}
\]
