代数余子式的由来/代数余子式为什么-1的系数是ⁱ⁺ʲ?/证明一个n阶行列式,如果其中第i行(或第j列)所有元素除aᵢⱼ外都为零,那么这行列式等于aᵢⱼ与它的代数余子式的乘积/证明行列式按行(列)展开法则:n(n>1)阶行列式等于它任意一行(列)的所有元素与它们对应的代数余子式的乘积的和。
代数余子式的由来/代数余子式为什么-1的系数是ⁱ⁺ʲ?/证明一个n阶行列式,如果其中第i行(或第j列)所有元素除aᵢⱼ外都为零,那么这行列式等于aᵢⱼ与它的代数余子式的乘积/证明行列式按行(列)展开法则:n(n>1)阶行列式等于它任意一行(列)的所有元素与它们对应的代数余子式的乘积的和。
前言:重在记录,可能出错。
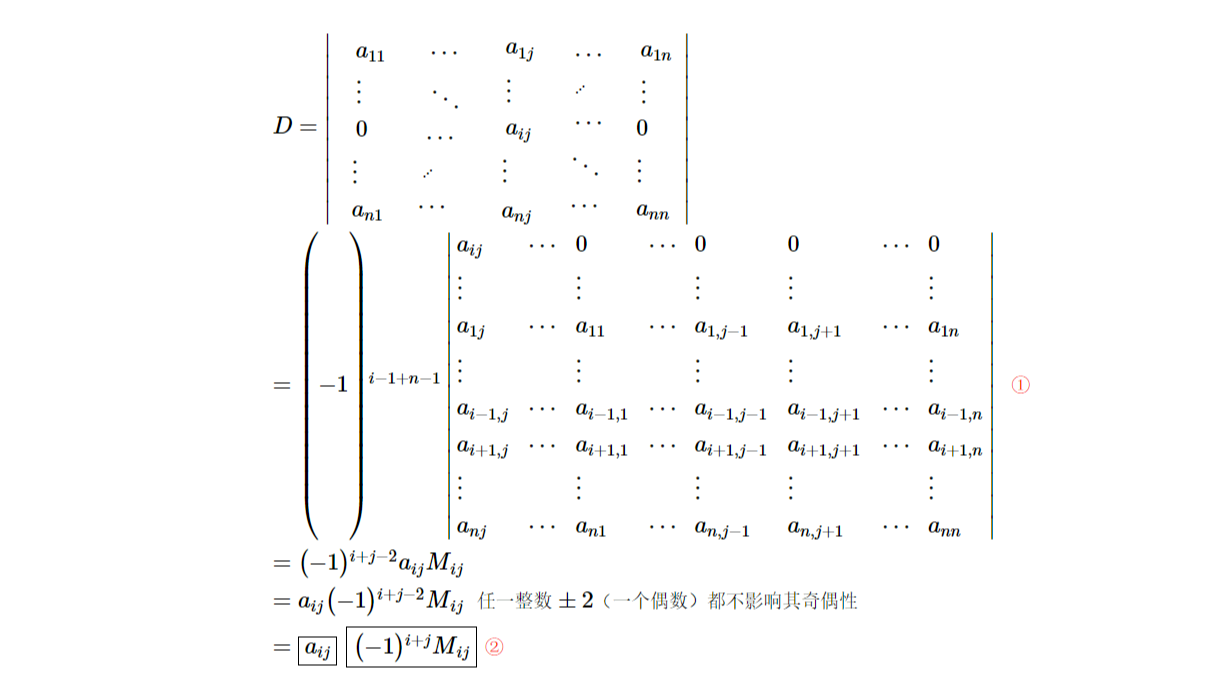
1. 代数余子式:(-1)ⁱ⁺ʲMᵢⱼ,Mᵢⱼ为余子式。当书本上第一次出现这个定义的时候,有人对这个ⁱ⁺ʲ感到疑惑,实际上,书本后面在证明引理——一个n阶行列式,如果其中第i行所有元素除aᵢⱼ外都为零,那么这行列式等于aᵢⱼ与它的代数余子式的乘积的时候已经给出了思路:
证:此处仅证第i行的情况,第j列情况的证明同理。
2. 怎么计算①式?
采用分块法:以第一行第一列元素仍为第一行第一列元素,将原行列式分块为二阶行列式D,第一行第二列块值为0,因此,此行列式的值为第一行第一列块值乘以第二行第二列块值。
3. 可见上述②式中已经出现了一个通项(代数余子式的)的身影,但是,这并不能使我们决定为它定义一个单独的名词。接下来证明行列式按行(列)展开法则:n(n>1)阶行列式等于它任意一行(列)的所有元素与它们对应的代数余子式的乘积的和。
证:此处仅证按行展开的情况,按列展开情况的证明同理。
此时,最后的结果同样出现一个通项(代数余子式的)身影,并且对于所有行列式有普遍性,因此我们赋予了(-1)ⁱ⁺ʲMᵢⱼ一个专有名称——代数余子式(algebraic complement minor),记作Aᵢⱼ。

