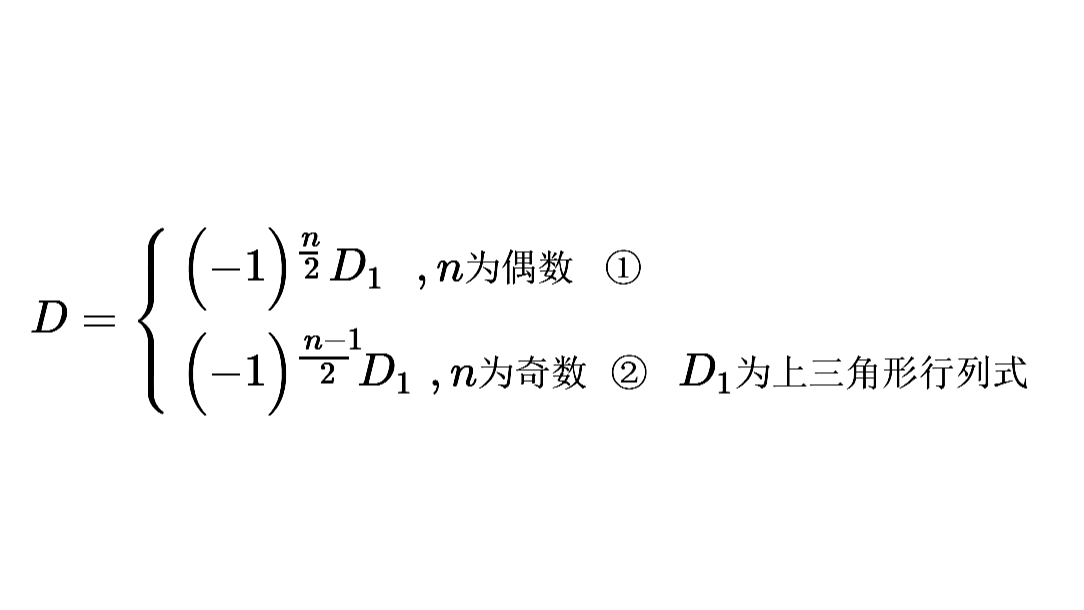
副三角形行列式转成上（下）三角形行列式为什么依次对换而不用第n行直接对换首行，第n-1行直接对换次行

副三角形行列式转成上（下）三角形行列式为什么依次对换而不用第n行直接对换首行，第n-1行直接对换次行

前言：重在记录，可能出错。

1. 简而言之，可以用第n行直接对换首行，第n-1行直接对换次行，直到行列式完全上下翻转。

但需要对n讨论奇偶。

2. 如果n是奇数，这种对换方法需要对换（变号）(n-1)/2次；如果n是偶数，则需要对换（变号）n/2次。列式，如下：

$$\mathit{D}=\{\begin{array}{l}(-1){}^{\frac{\mathit{n}}{2}}\mathit{D}{}_1,\mathit{n}\text{为}\text{偶}\text{数}\text{①}\\ (-1){}^{\frac{\mathit{n}-1}{2}}\mathit{D}{}_1,\mathit{n}\text{为}\text{奇}\text{数}\text{②}\mathit{D}{}_1\text{为}\text{上}\text{三}\text{角}\text{形}\text{行}\text{列}\text{式}\end{array}$$

3. 怎么统一？这里需要借用自然数的奇偶特性——奇数乘以一个自然数，结果不改变此自然数的奇偶性。

因此，我们给①式乘上一个奇数n-1，给②式乘上一个奇数n，不改变①、②式的值。列式，如下：

$$\mathit{D}=\{\begin{array}{l}(-1){}^{\frac{\mathit{n}}{2}\bullet (\mathit{n}-1)}\mathit{D}{}_1,\mathit{n}\text{为}\text{偶}\text{数}\text{③}\\ (-1){}^{\frac{\mathit{n}-1}{2}\bullet \mathit{n}}\mathit{D}{}_1,\mathit{n}\text{为}\text{奇}\text{数}\text{④}\mathit{D}{}_1\text{为}\text{上}\text{三}\text{角}\text{形}\text{行}\text{列}\text{式}\end{array}$$

显然，③、④式在形式上已经统一，不再受n的奇偶性的影响，得到：

$$\mathit{D}=(-1){}^{\frac{\mathit{n}(\mathit{n}-1)}{2}}\mathit{D}{}_1=(-1){}^{\frac{\mathit{n}(\mathit{n}-1)}{2}}\mathit{a}{}_{1\mathit{n}}\mathit{a}{}_{2,\mathit{n}-1}⸳⸳⸳\mathit{a}{}_{\mathit{n}1}$$

4. 既然证明了这样求也行的，再说说其他的求法。

(1)、根据n阶行列式的定义——$$\sum (-1){}^{\mathit{t}}\mathit{a}{}_{1\mathit{p}{}_1}\mathit{a}{}_{2\mathit{p}{}_2}⸳⸳⸳\mathit{a}{}_{\mathit{n}\mathit{p}{}_{\mathit{n}}}\text{t}\text{为}\mathit{p}{}_1\mathit{p}{}_1⸳⸳⸳\mathit{p}{}_{\text{n}}\text{排}\text{列}\text{的}\text{逆}\text{序}\text{数}$$

类比上（下）三角形行列式值的推导，上式中不含0的项只有$$(-1){}^{\mathit{t}}\mathit{a}{}_{1\mathit{n}}\mathit{a}{}_{2,\mathit{n}-1}⸳⸳⸳\mathit{a}{}_{\mathit{n}{}_1}$$

t=0+1+···+(n-1)=n(n-1)/2 　　等差数列求和

因此：

$$\mathit{D}=(-1){}^{\frac{\mathit{n}(\mathit{n}-1)}{2}}\mathit{D}{}_1=(-1){}^{\frac{\mathit{n}(\mathit{n}-1)}{2}}\mathit{a}{}_{1\mathit{n}}\mathit{a}{}_{2,\mathit{n}-1}⸳⸳⸳\mathit{a}{}_{\mathit{n}1}$$

(2)、转换过程既然是上下翻转，那就应该是乘以一个行列式上下翻转系数：将第n行反复进行相邻对换到首行需要n-1次，再将之后的行列式第n行反复进行相邻对换到次行需要n-2次，因此副三角形行列式反转成上（下）三角形行列式需要n(n-1)/2次（每次仅允许相邻对换）。符号最终为(-1)^[n(n-1)/2]。

(3)、使用代数余子式求行列式的值，层层拆开后发现，也还是副对角线的数相乘，然后求符号的正负，这个很简单，就不细说了。