树链剖分
树链剖分是个好东西呀
我挺喜欢用树剖求\(LCA\)的
因为我不太会打倍增
接下来就稍微说一下树剖的实现
首先我们先引入几个概念：
- 重儿子：这个点的子树中\(siz\)最大的
- 轻儿子：子节点中除了重儿子的节点都是轻儿子
- 重边：与重儿子相连的边
- 轻边：与轻儿子相连的边
- 重链：重边组成的链叫重链
然后我们我还要知道跳重链是个什么东东
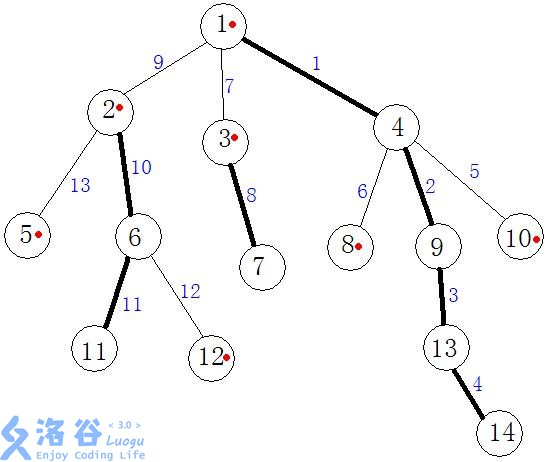
就以这张我在网上扒的图片为例吧
这张图里的所有黑色加粗的边都是重边
我们用\(top\)记录一下当前这条重链的顶端就好了
例如：\(14\)那条重链的顶端就是\(1\),而\(11\)那条重链的顶端就是\(2\)
然后我们就可以根据这个来进行操作了
求\(LCA\)
求\(LCA\)的主要思路就是跳重链，直到两个点跳到同一条重链上为止，并且深度较小的那个就是要求的\(LCA\)，我们可以模拟求一下\(12\)和\(7\)的\(LCA\)
首先我们可以知道\(7\)和\(12\)并不在同一条重链上，所以我们要通过跳重链来使这两个点跳到一条重链上去
我们要让所处链的\(top\)深的先跳，直到跳到与那个浅的\(top\)同高或比它浅为止
我们就可以看出我们就要让\(12\)先跳到\(2->6->11\)这条重链上去（即跳到\(fa[top]\)上去），然后我们就可以在让\(12\)向上跳，我们就会发现，
它会跳到了\(1\)的位置，然后我们就可以让\(7\)跳了，\(7\)跳一次重链就到达了\(1\)，然后就可以得出结论\(7\)和\(12\)的\(LCA\)就是\(1\)
我们简化为：
\[12->6->1
\]
\[7->1
\]
然后就看一道模板题
题目
其实就是求\(LCA\)的裸题（下面会有两种代码，但是我个人比较爱写树剖的这个）
倍增版:
#include<bits/stdc++.h>
using namespace std;
const int N = 500000 + 5;
int n, m, root, head[N], cnt, hig[N], f[N][21];
struct node{
int u, v, nxt;
}edge[N << 1];
void add(int u, int v){
edge[++ cnt].u = u;
edge[cnt].v = v;
edge[cnt].nxt = head[u];
head[u] = cnt;
}
void add_tree(int x){
for(int i = 1; i <= 19; i ++){
f[x][i] = f[f[x][i - 1]][i - 1];
}
for(int i = head[x]; i; i = edge[i].nxt){
if(edge[i].v == f[x][0]) continue;
f[edge[i].v][0] = x;
hig[edge[i].v] = hig[x] + 1;
add_tree(edge[i].v);
}
}
int ask(int x, int y){
if(hig[x] < hig[y]) swap(x, y);
for(int i = 19; i >= 0; i --){
if(hig[f[x][i]] >= hig[y]) x = f[x][i];
}
if(x == y) return x;
for(int i = 19; i >= 0; i--){
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
}
return f[x][0];
}
int read(){
int op = 0, opp = 1; char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') opp = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){ op = (op << 1) + (op << 3) + (ch - '0'); ch = getchar();}
return op * opp;
}
int main(){
n = read(), m = read(), root = read();
for(int i = 1, x, y; i < n; i ++){
x = read(), y = read();
add(x, y); add(y, x);
}
hig[root] = 1;
add_tree(root);
for(int i = 1, x, y; i <= m; i ++){
x = read(), y = read();
printf("%d\n", ask(x, y));
}
return 0;
}
树剖版
#include<bits/stdc++.h>
using namespace std;
const int N = 500000 + 5;
int n, m, root, head[N], fa[N], top[N], cnt, hig[N], siz[N], hev[N];
struct node{
int u, v, nxt;
}edge[N << 1];
void add(int u, int v){
edge[++ cnt].u = u;
edge[cnt].v = v;
edge[cnt].nxt = head[u];
head[u] = cnt;
}
void dfs1(int x){
siz[x] = 1;
for(int i = head[x]; i; i = edge[i].nxt){
int to = edge[i].v;
if(to == fa[x]) continue;
fa[to] = x;
hig[to] = hig[x] + 1;
dfs1(to);
siz[x] += siz[to];
if(siz[to] > siz[hev[x]]) hev[x] = to;
}
}
void dfs2(int x, int topx){
top[x] = topx;
if(hev[x]) dfs2(hev[x], topx);
for(int i = head[x]; i; i = edge[i].nxt){
int to = edge[i].v;
if(to == fa[x] || to == hev[x]) continue;
dfs2(to, to);
}
}
int ask(int x, int y){
while(top[x] != top[y]){
if(hig[top[x]] < hig[top[y]]) swap(x, y);
x = fa[top[x]];
}
return hig[x] < hig[y] ? x : y;
}
int read(){
int op = 0, opp = 1; char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') opp = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){ op = (op << 1) + (op << 3) + (ch - '0'); ch = getchar();}
return op * opp;
}
int main(){
n = read(), m = read(), root = read();
for(int i = 1, x, y; i < n; i ++){
x = read(), y = read();
add(x, y); add(y, x);
}
hig[root] = 1;
dfs1(root);
dfs2(root, root);
for(int i = 1, x, y; i <= m; i ++){
x = read(), y = read();
printf("%d\n", ask(x, y));
}
return 0;
}
求\(LCA\)其实有很多种方法的，只不过因为\(Tethys\)太菜了，只会这两种，所以就先占个坑吧
