11.9noip模拟赛?
Problem 1 Graph (graph.cpp/c/pas)
【题目描述】
给出 N 个点,M 条边的有向图,对于每个点 v,求 A(v) 表示从点 v 出发,能到达的编号最大的点。
【输入格式】
第 1 行,2 个整数 N,M。 接下来 M 行,每行 2 个整数 Ui,Vi,表示边 Ui, Vi。点用 1,2,...,N 编号。
【输出格式】
N 个整数 A(1),A(2),...,A(N)。
【样例输入】
4 3
1 2
2 4
4 3
【样例输出】
4 4 3 4
【数据范围】
对于 60% 的数据,1 ≤ N,K ≤ 10^3
对于 100% 的数据,1 ≤ N,M ≤ 10^5。
题解:
反向建图,从大到小向下搜
代码:

#include<cstdio> #include<iostream> using namespace std; const int M = 100010; int n,m,pre[M*4],to[M*4],len[M*4],head[M],u,v,num,w[M],vis[M],cd[M]; void add(int u,int v) { pre[++num]=head[u]; to[num]=v; head[u]=num; } void dfs(int s) { if(vis[s]) return ; vis[s]=1; for(int i=head[s]; i; i=pre[i]) { int v=to[i]; if(!vis[v]) { w[v]=max(w[v],w[s]); dfs(v); } } } int main() { freopen("graph.in","r",stdin); freopen("graph.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1; i<=m; i++) { scanf("%d%d",&u,&v); add(v,u); } for(int i=1; i<=n; i++) w[i]=i; for(int i=n; i>=1; i--) dfs(i); for(int i=1; i<=n; i++) printf("%d ",w[i]); fclose(stdin); fclose(stdout); return 0; }
Problem 2 Incr(incr.cpp/c/pas)
【题目描述】
数列 A1,A2,...,AN,修改最少的数字,使得数列严格单调递增。
【输入格式】
第 1 行,1 个整数 N
第 2 行,N 个整数 A1,A2,...,AN
【输出格式】
1 个整数,表示最少修改的数字
【样例输入】
3
1 3 2
【样例输出】
1
【数据范围】
对于 50% 的数据,N ≤ 10^3
对于 100% 的数据,1 ≤ N ≤ 10^5,1 ≤ Ai ≤ 10^9
题解:
最长上升子序列的错误性: 该题要求求得单调递增序列,所以数字不能相同。 如果直接求得最长上升子序列那么会出现错误,因为两个数中间已经不能放数了,因为保证不重复,如2,3之间就不可以再放入数字,所以直接求得单调上升序列会使得错误的解出现,而将其转换成严格不降之后是肯定可以放入数字的,因为可以重复,所以只要找出转换后序列的最长不降序列,再用总数减去即可得到解。中间必然可以放下数字,不会出现非法的解的情况。因为数据范围较大,所以不能采用传统的O(n^2)的算法,采用O(nlog(n))的算法。
参考博客:http://blog.csdn.net/xuxianbo123/article/details/49516323
式子的正确性:
题目说严格上升,也就是对每个 i<j 都必须 a[i]-i <=a[j]-j
下面证明这个式子的正确性:
严格单调递增序列有 a[i+1]-a[i] > 0
由于是整数,所以 a[i+1]-a[i] >= 1
稍微变形也就是 a[i]-i <= a[i+1]-(i+1)
于是由不等式的传递性,a[i]-i <= a[i+1]-(i+1) <= a[i+2]-(i+2) <= ..... <=a[j]-j
于是我们令b[i]=a[i]-i,则a[i]的严格递增等价于b[i]的单调不降
所以只需要求出b[i]的最长不下降子序列,把不在序列中的那些数b[i]都改成符合条件的数(比如说和左边最近一个在最长不下降子序列中的b[j]相等)就能满足题意了
当然,我们并不需要求出具体的修改方案,我们只需要求出最长不下降的长度K,输出N-K即可
参考博客:http://blog.csdn.net/greatwjj/article/details/14518345
代码:

#include<cstdio> #include<iostream> using namespace std; const int M = 100010; int f[M],n,a[M],maxn; int solve() { for(int i=1; i<=n; i++) f[i]=1; for(int i=1; i<=n; i++) for(int j=1; j<=i-1; j++) if(a[j]<a[i]) f[i]=max(f[i],f[j]+1); for(int i=1; i<=n; i++) if(maxn<f[i]) maxn=f[i]; return maxn; } int main() { freopen("incr.in","r",stdin); freopen("incr.out","w",stdout); scanf("%d",&n); for(int i=1; i<=n; i++) scanf("%d",&a[i]); int ans=solve(); printf("%d",n-ans); fclose(stdin); fclose(stdout); return 0; }

#include<iostream> #include<cstdio> #define maxn 100010 using namespace std; int n,v[maxn],st[maxn],top=0; int find(int x) { int l=0,r=top,res=0; while(l<=r) { int mid=(l+r+1)>>1; if(st[mid]<=x) { res=mid; l=mid+1; } else r=mid-1; } return res; } int main() { freopen("incr.in","r",stdin); freopen("incr.out","w",stdout); scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%d",&v[i]); v[i]-=i; } st[0]=-0x7fffffff,st[1]=v[1]; top=1; for(int i=2; i<=n; i++) { int k=find(v[i]); st[k+1]=v[i]; top=max(top,k+1); } printf("%d",n-top); fclose(stdin); fclose(stdout); return 0; }
Problem 3 Permutation (permutation.cpp/c/pas)
【题目描述】
将 1 到 N 任意排列,然后在排列的每两个数之间根据他们的大小关系插入“>”和“<”。问在所有排列中,有多少个排列恰好有K个“<”。
例如排列(3, 4, 1, 5, 2)
3 < 4 > 1 < 5 > 2
共有2个“<”
【输入格式】
N,K
【输出格式】
答案
【样例输入】
5 2
【样例输出】
66
【数据范围】
20%:N <= 10
50%:答案在0..2^63-1内
100%:K < N <= 100
题解:
这绝对不是一道暴力题。
很容易就能想到,从1到n将数字一个个添加进去,同时每添加一个数字,< 要么多一个,要么不变。因此,我们用数组f[i][j]表示前i个数字的所有排列中有j个<的排列个数。由于每添加一个数字只能增加一个<或者不增加,因此f[i][j]只能由f[i-1][j-1]和f[i-1][j]推出来。(f[i-1][j-1]考虑<增多的情况,f[i-1][j]考虑不变的情况)。
那么怎样添加可以使<增多呢?首先要明确一点:要添加进排列的数字一定比排列中所有的数字都大,因为我们是从1到n逐个添加的。然后,能够添加的位置有四个:1.第一个数字前,2.最后一个数字后( < 会增多),3.添加在>关系的两个数字间,3.添加在<关系的两个数字间。
来看一下后两种情况:
3.添加在>关系的两个数字间:
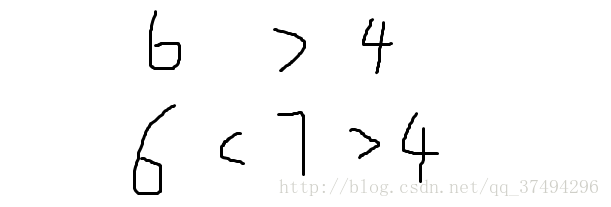
很明显,<符号多了一个。
4.添加在<关系的两个数字间: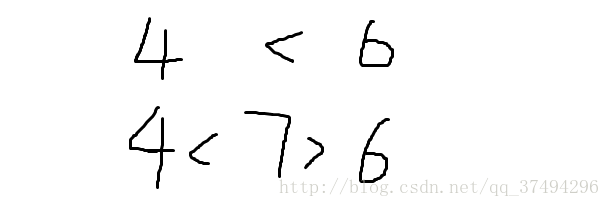
很明显,<数目不变。同样的,添加在最前面,<不变,添加在最后面会增多。
先看递推式再解释:f[i][j]=(f[i-1][j-1]*(i-j)%2012+f[i-1][j]*(j+1)%2012)%2012。
首先考虑f[i-1][j-1],很明显,这要求将i添加后<多一个,已知,每一种排列有j-1个<,对应的,就有(i-2-(j-1))=(i-j-1)个>,由此前的图可知将数字添加在有>两个数字间 会多一个<,因此f[i][j]+=f[i-1][j-1]*(i-j-1)。在考虑添加在末尾的情况,f[i][j]+=f[i-1][j-1]*(i-j-1)+f[i-1][j-1],合并为f[i-1][j-1]*(i-j)。
同样的,对于f[i-1][j]我们考虑<不变的情况,即添加在<关系的两个数字间或者最前面,易得为f[i-1][j]*(j+1)。
最后注意赋初值的问题。
100%的数据会用到高精!!!
参考博客:http://blog.csdn.net/qq_37494296/article/details/77530027
代码:

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,k,a[1010],b[1010],c[1010]; struct node{ int len,zu[1010]; node operator * (const int x)const{ node res;res.len=0; memset(a,0,sizeof(a)); memset(b,0,sizeof(b)); for(int i=1,j=len;i<=len;i++,j--)a[i]=zu[j]; for(int i=1;i<=len;i++){ b[i]+=a[i]*x; b[i+1]+=b[i]/10; b[i]%=10; } int l=len; while(b[l+1]){ l++; b[l+1]=b[l]/10; b[l]%=10; } res.len=l; for(int i=1,j=l;i<=l;i++,j--)res.zu[i]=b[j]; return res; } node operator + (const node x)const{ node res;res.len=0; memset(a,0,sizeof(a)); memset(b,0,sizeof(b)); memset(c,0,sizeof(c)); for(int i=1,j=len;i<=len;i++,j--)a[i]=zu[j]; for(int i=1,j=x.len;i<=x.len;i++,j--)b[i]=x.zu[j]; int l=max(len,x.len); for(int i=1;i<=l;i++){ c[i]+=a[i]+b[i]; c[i+1]+=c[i]/10; c[i]%=10; } while(c[l+1]){ l++; c[l+1]=c[l]/10; c[l]%=10; } res.len=l; for(int i=1,j=l;i<=l;i++,j--)res.zu[i]=c[j]; return res; } }f[110][110]; int main(){ freopen("permutation.in","r",stdin);freopen("permutation.out","w",stdout); // freopen("Cola.txt","r",stdin); scanf("%d%d",&n,&k); for(int i=1;i<=n;i++){ f[i][0].len=1; f[i][0].zu[1]=1; } for(int i=2;i<=n;i++) for(int j=1;j<=min(i-1,k);j++) f[i][j]=((f[i-1][j]*(j+1))+(f[i-1][j-1]*(i-j))); for(int i=1;i<=f[n][k].len;i++)printf("%d",f[n][k].zu[i]); fclose(stdin);fclose(stdout); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号