tarjan
什么是缩点?
当我们在求出强连通分量之后,我们可以把同一个强连通分量里的点当成新图里的一个新点,然后如果原图中两个不在同一个强连通分量的点有连边的话,那么他们所对应的新点也有连边。
我们可以知道,新图一定是一个有向无环图(DAG)。
void Shrink_point() { for(int i=1; i<=n; i++) for(int j=head[i]; j; j=edge[j].pre) { int to=edge[j].to; if(col[i]!=col[to]) add(col[i],col[to]); } }
P3387 【模板】缩点
题目背景
缩点+DP
题目描述
给定一个n个点m条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
输入输出格式
输入格式:
第一行,n,m
第二行,n个整数,依次代表点权
第三至m+2行,每行两个整数u,v,表示u->v有一条有向边
输出格式:
共一行,最大的点权之和。
输入输出样例
2 2
1 1
1 2
2 1
2
说明
n<=10^4,m<=10^5,|点权|<=1000
算法:Tarjan缩点+DAGdp
/*----------------------------------------------------*/
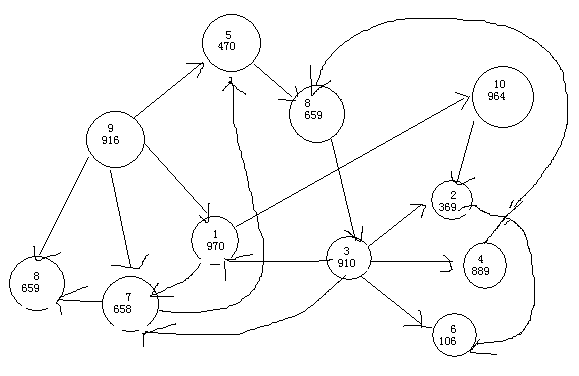
#样例:
10 20
970 369 910 889 470 106 658 659 916 964
3 2
3 6
3 4
9 5
8 3
5 8
9 1
9 7
9 8
7 5
3 7
7 8
1 7
10 2
1 10
4 8
2 6
3 1
3 5
8 5
#输出:
6911
/*----------------------------------------------------*/
题解:
Tarjan缩点+最短路(spfa)
为何缩点?—— 因为可以重复经过点,所以一个点所在的强联通分量必定可以到达,所以直接缩点即可
暴力从每个点跑spfa,取最大权值
代码:

#include<queue> #include<cstdio> #include<cstring> #include<iostream> using namespace std; const int M = 100010; int n,m,dis[M],value[M],ans,num_edge,dfn[M],low[M]; int Right[M],head[M]; struct Edge { int pre,to,len; } edge[M*4]; void add(int u,int v) { edge[++num_edge].pre = head[u]; edge[num_edge].to = v; head[u]=num_edge; } int numb_edge,head1[M]; struct Edge1 { int pre,to,len; } edge1[M*3]; void add1(int u,int v) { edge1[++numb_edge].pre = head1[u]; edge1[numb_edge].to = v; head1[u]=numb_edge; } int dfs_num,stack[M],top,col[M],col_num; bool vis[M]; void tarjan(int x) { dfn[x]=low[x]=++dfs_num; stack[++top]=x; vis[x]=1; for(int i=head[x]; i; i=edge[i].pre) { int to=edge[i].to; if(!dfn[to]) { tarjan(to); low[x]=min(low[x],low[to]); } else if(vis[to]) { low[x]=min(low[x],dfn[to]); } } if(low[x]==dfn[x]) { ++col_num; vis[x]=false; while(stack[top+1]!=x) { col[stack[top]]=col_num; value[col_num]+=Right[stack[top]]; ans=max(ans,value[col_num]); vis[stack[top--]]=false; } } } void Shrink_point() { for(int i=1; i<=n; i++) for(int j=head[i]; j; j=edge[j].pre) { int to=edge[j].to; if(col[i]!=col[to]) add1(col[i],col[to]); } } bool v[M]; void spfa(int x) { memset(dis,0,sizeof(dis)); memset(v,0,sizeof(v)); dis[x]=value[x]; queue<int>q; q.push(x); v[x]=true; while(!q.empty()) { int fst=q.front(); q.pop(); v[fst]=false; for(int i=head1[fst]; i; i=edge1[i].pre) { int to=edge1[i].to; if(dis[to]<dis[fst]+value[to]) { dis[to]=dis[fst]+value[to]; if(!v[to]) { v[to]=true; q.push(to); } } } } for(int i=1; i<=col_num; i++) ans=max(ans,dis[i]); } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) scanf("%d",&Right[i]); int u,v; for(int i=1; i<=m; i++) { scanf("%d%d",&u,&v); add(u,v); } for(int i=1; i<=n; i++) if(!dfn[i]) tarjan(i); Shrink_point(); for(int i=1; i<=col_num; i++) spfa(i); printf("%d",ans); return 0; }
割点:如果在图G中去掉一个顶点(自然同时去掉与该顶点相关联的所有边)后,该图的连通分支数增加,则称该顶点为G的割点
访问路径可以绘制成下图(绿边为访问未访问顶点时经过的边,红边为访问已访问节点时经过的边):
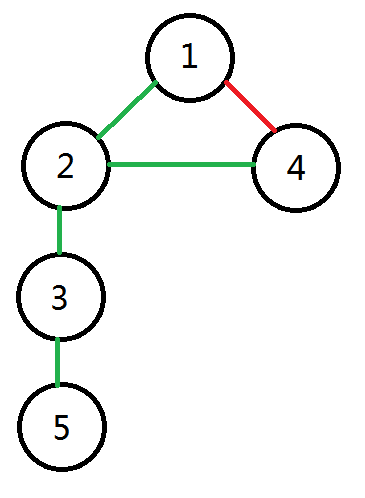
我们把上图称为DFS搜索树(DFS tree),上图中的绿边称为树边(tree edge),红边称为回边(back edge)。通过回边可以从一个点返回到之间访问过的顶点。
首先选定一个根节点,从该根节点开始遍历整个图(使用DFS)。
对于根节点,判断是不是割点很简单——计算其子树数量,如果有2棵即以上的子树,就是割点。因为如果去掉这个点,这两棵子树就不能互相到达。
对于非根节点,判断是不是割点就有些麻烦了。我们维护两个数组dfn[]和low[],
dfn[u]表示顶点u第几个被(首次)访问,
low[u]表示顶点u及其子树中的点,通过非父子边(回边),能够回溯到的最早的点(dfn最小)的dfn值(但不能通过连接u与其父节点的边)。对于边(u, v),如果low[v]>=dfn[u],此时u就是割点。
但这里也出现一个问题:怎么计算low[u]。
假设当前顶点为u,则默认low[u]=dfn[u],即最早只能回溯到自身。
有一条边(u, v),如果v未访问过,继续DFS,DFS完之后,low[u]=min(low[u], low[v]);
如果v访问过(且u不是v的父亲),就不需要继续DFS了,一定有dfn[v]<dfn[u],low[u]=min(low[u], dfn[v])。
P3388 【模板】割点(割顶)
题目背景
割点
题目描述
给出一个n个点,m条边的无向图,求图的割点。
输入输出格式
输入格式:
第一行输入n,m
下面m行每行输入x,y表示x到y有一条边
输出格式:
第一行输出割点个数
第二行按照节点编号从小到大输出节点,用空格隔开
输入输出样例
6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6
1
5
说明
n,m均为100000
tarjan 图不一定联通!!!
代码:

#include<cstdio> #include<iostream> using namespace std; const int M = 100010; int dfn[M],low[M]; int dfs_num,top,vis[M],col_num,n,m; int head[M],num_edge,tot; bool cut[M]; struct Edge { int pre,to,len; } edge[M*4]; void add(int u,int v) { edge[++num_edge].pre = head[u]; edge[num_edge].to = v; head[u] = num_edge; } void tarjan(int x,int fa) { tot=0; dfn[x]=low[x]=++dfs_num; for(int i=head[x]; i; i=edge[i].pre) { int to=edge[i].to; if(!dfn[to]) { tarjan(to,fa); low[x]=min(low[x],low[to]); if(low[to]>=dfn[x]&&x!=fa) cut[x]=true; if(x==fa) tot++; } low[x]=min(low[x],dfn[to]); } if(tot>=2&&x==fa) cut[x]=true; } int main() { scanf("%d%d",&n,&m); int x,y; for(int i=1; i<=m; i++) { scanf("%d%d",&x,&y); add(x,y); add(y,x); } for(int i=1; i<=n; i++) if(!dfn[i]) tarjan(i,i); int ans=0; for(int i=1; i<=n; i++) if(cut[i]) ans++; printf("%d\n",ans); for(int i=1; i<=n; i++) if(cut[i]) printf("%d ",i); return 0; }
自己选的路,跪着也要走完!!!



